题目内容
10.已知m2-6m-1=0,求2m2-6m+$\frac{1}{m^2}$=39.分析 依据等式的性质由m2-6m-1=0得到2m2-6m=1+m2,$m-\frac{1}{m}=6$,故此所求代数式=1+m2+$\frac{1}{{m}^{2}}$,然后利用完全平方公式科将所求代数式变形为1$+(m-\frac{1}{m})^{2}$+2,最后代入数值进行计算即可.
解答 解:由m2-6m-1=0得;2m2-6m=1+m2,$m-\frac{1}{m}=6$,
∴2m2-6m+$\frac{1}{m^2}$=1+m2+$\frac{1}{{m}^{2}}$=1$+(m-\frac{1}{m})^{2}$+2=1+62+3=39.
故答案为:39.
点评 本题主要考查的是完全平方公式的应用、等式的性质,由m2-6m-1=0得到2m2-6m=1+m2是解题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1. 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
 如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )
如图,A,B是⊙O的直径,C、D在⊙O上,$\widehat{AD}$=$\widehat{DC}$,若∠DAB=58°,则∠CAB=( )| A. | 20° | B. | 22° | C. | 24° | D. | 26° |
18.请你观察下列各式,用含自然数n(n≧1)的代数式填空,并在表格右侧说明你的理由?
| $\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$ | 理由: |
| $\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$ | |
| $\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$ | |
| … | |
| $\sqrt{n+\frac{1}{n+2}}$=(n+1)$\sqrt{\frac{1}{n+2}}$ |
5.2015年8月初,某学生用品专卖店以每个50元的价格购进800个芭蕾牌书包,第一周以单价80元销售,售出了200个;第二周如果单价不变,预计仍可售出200个,该专卖店为了增加销售量.决定从第二周开始降价销售,据市场调查,若单价每降低1元,就可多售出10个,但最低单价应高于购进价.待第二周结束后,专卖店再对剩余书包进行一次性清仓销售,清仓时按进价八折销售,设第二周的单价降低x元.
(1)填写下表(不需要化简)
(2)如果专卖店希望通过销售这批书包获利9000元,那么第二周的单价应是多少?
(1)填写下表(不需要化简)
| 时间 | 第一周 | 第二周 | 清仓 |
| 单价(元) | 80 | 80-x | 40 |
| 销售量(个) | 200 | 200+10x | 400-10x |
2.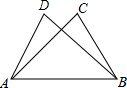 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
 如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )
如图,△ABC≌△BAD,点A和点B,点C和点D是对应点,如果AB=6cm,BD=5cm,AD=4cm,那么BC的长是( )| A. | 3cm | B. | 4cm | C. | 5cm | D. | 6cm |
20.若|a|=|-4|,则a的值是( )
| A. | 4 | B. | ±4 | C. | -4 | D. | -8 |

 如图,数轴上的点A,B分别表示数-1和2,点C是线段AB的中点,则点C表示的数是0.5.
如图,数轴上的点A,B分别表示数-1和2,点C是线段AB的中点,则点C表示的数是0.5.