题目内容
6. 如图,在梯形ABCD中,对角线AC⊥BD,且AC=13,BD=8,则梯形ABCD的面积是52.
如图,在梯形ABCD中,对角线AC⊥BD,且AC=13,BD=8,则梯形ABCD的面积是52.
分析 过点B作BF∥AC交BC的延长线于F,则四边形ACFB是平行四边形,得出BF=AC=12,即可得到结论.
解答  解:过点B作BF∥AC交DC的延长线于F,BE⊥DC于E,如图所示:
解:过点B作BF∥AC交DC的延长线于F,BE⊥DC于E,如图所示:
则四边形ACFB是平行四边形,
∴BF=AC=13,CF=AB,
∵BD⊥AC,
∴BF⊥BD,
∴∠DBF=90°,
∵S△BDF=$\frac{1}{2}$BF•BE=$\frac{1}{2}$(DC+CF)•BE=$\frac{1}{2}$(DC+AB)•BE=$\frac{1}{2}$BF•BD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×13×8=52.
故答案为:52.
点评 本题考查了梯形的性质、平行四边形的判定与性质、勾股定理、三角形面积的计算;熟练掌握梯形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
18.如图是正方体表面展开图,如果将其合成原来的正方体如图时,与点重合的两个点应该是( )


| A. | S和Z | B. | T和Y | C. | T和V | D. | U和Y |
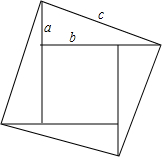 如图所示,现用三边长分别为a,b,c的四个全等的直角三角形拼成正方形,利用以下方法验证:a2+b2=c2,在图中,边长为c的大正方形的面积为(a2+b2)或c2.
如图所示,现用三边长分别为a,b,c的四个全等的直角三角形拼成正方形,利用以下方法验证:a2+b2=c2,在图中,边长为c的大正方形的面积为(a2+b2)或c2. 如图小方做了一个方形框架,发现很容易变形,请你帮他选择一个最好的加固方案( )
如图小方做了一个方形框架,发现很容易变形,请你帮他选择一个最好的加固方案( )



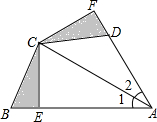 在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,问BE与DF是否相等?为什么?
在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,问BE与DF是否相等?为什么?