题目内容
15.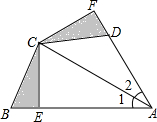 在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,问BE与DF是否相等?为什么?
在△ABC中,CE⊥AB于E,在△ABC外作∠CAD=∠CAB,过C作CF⊥AD,交AD的延长线于F,且∠FDC=∠B,问BE与DF是否相等?为什么?
分析 根据角平分线上的点到角的两边距离相等可得CE=CF,然后利用“角角边”证明△CDF和△CBE全等,再根据全等三角形对应边相等证明即可.
解答 解:BE=DF,理由如下:
∵∠CAD=∠CAB,CF⊥AD,CE⊥AB,
∴CE=CF,
在△CDF和△CBE中,
$\left\{\begin{array}{l}{∠F=∠CEB=90°}\\{∠CDF=∠B}\\{CE=CF}\end{array}\right.$,
∴△CDF≌△CBE(AAS),
∴BE=DF.
点评 本题考查了全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记性质并确定出全等三角形是解题的关键.

练习册系列答案
相关题目
3.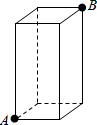 如图一只蚂蚁从长宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
如图一只蚂蚁从长宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
 如图一只蚂蚁从长宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
如图一只蚂蚁从长宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )| A. | 13cm | B. | 10cm | C. | 14cm | D. | 无法确定 |
20.已知2a-b=2,那么代数式4a2-b2-4b的值是( )
| A. | 6 | B. | 4 | C. | 2 | D. | 0 |
5.若(x-3)2=x2-mx+9,则m的值是( )
| A. | 3 | B. | 6 | C. | 9 | D. | -6 |
 如图,在梯形ABCD中,对角线AC⊥BD,且AC=13,BD=8,则梯形ABCD的面积是52.
如图,在梯形ABCD中,对角线AC⊥BD,且AC=13,BD=8,则梯形ABCD的面积是52. 如图,是一条水平铺设的直径为2米的通水管道横截面,其水面宽度为1.6米,求这条管道中此时水的最大深度.
如图,是一条水平铺设的直径为2米的通水管道横截面,其水面宽度为1.6米,求这条管道中此时水的最大深度.