题目内容
3. 如图,已知∠ADE=70°,DF平分∠ADE,∠2=35°,求证:DF∥BE.
如图,已知∠ADE=70°,DF平分∠ADE,∠2=35°,求证:DF∥BE.
分析 由∠ADE=70°,DF平分∠ADE,可得∠1=$\frac{1}{2}$∠ADE=35°,然后由∠2=35°,可得∠2=∠1,然后由内错角相等,两直线平行,即可证明DF∥BE.
解答 证明:∵DF平分∠ADE,
∴∠1=$\frac{1}{2}$∠ADE,
∵∠ADE=70°,
∴∠1═35°
∵∠2=35°,
∴∠2=∠1,
∴DF∥BE.
点评 此题考查了平行线的判定,利用角判断两直线平行的方法有:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
11. 如图所示,能推出AD∥BC的是( )
如图所示,能推出AD∥BC的是( )
 如图所示,能推出AD∥BC的是( )
如图所示,能推出AD∥BC的是( )| A. | ∠DAB+∠D=180° | B. | ∠2=∠4 | C. | ∠1=∠3 | D. | ∠CBE=∠BCD |
12. 如图,在四边形ABCD中,∠1=∠2,∠A=60°,则∠ADC=( )
如图,在四边形ABCD中,∠1=∠2,∠A=60°,则∠ADC=( )
 如图,在四边形ABCD中,∠1=∠2,∠A=60°,则∠ADC=( )
如图,在四边形ABCD中,∠1=∠2,∠A=60°,则∠ADC=( )| A. | 65° | B. | 60° | C. | 110° | D. | 120° |
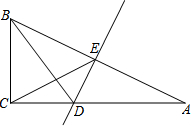 如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC.
如图,在Rt△ABC中,∠C=Rt∠,AB的垂直平分线交AC于点D,交AB于点E,BD平分∠ABC. 如图,已知直线AB∥CD,∠1=50°,那么∠2=130°.
如图,已知直线AB∥CD,∠1=50°,那么∠2=130°. 某中学的铅球场如图所示,已知扇形OAB的面积是72π米2,弧AB的长度为6π米,那么圆心角为45度.
某中学的铅球场如图所示,已知扇形OAB的面积是72π米2,弧AB的长度为6π米,那么圆心角为45度.