��Ŀ����
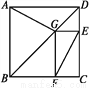
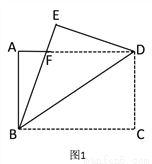
��ͼ 1����һ�ž���ֽƬ ABCD ���ŶԽ��� BD �����۵������� C �䵽�� E ����BE �� AD �ڵ� F.
��1����֤����BDF �ǵ��������Σ�
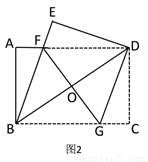
��2����ͼ 2������ D �� DG��BE���� BC �ڵ� G������ FG �� BD �ڵ� O.
���ж��ı��� BFDG ����״����˵�����ɣ�
���� AB=6��AD=8���� FG �ij�Ϊ_____.
��ϰ��ϵ�д�
�����Ŀ


 ����2����ʽ
����2����ʽ ����������⣮
����������⣮ �ĶԽ���
�ĶԽ���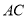 ��
��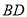 �ཻ�ڵ�
�ཻ�ڵ�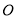 �����
�����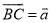 ��
�� 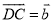 ����ô
����ô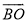 ����( )
����( )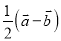 �� B.
�� B. 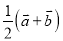 �� C.
�� C. 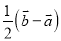 �� D.
�� D. 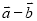 ��
��