题目内容
2.若abc≠0,求$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$的可能取值.分析 由已知可得:a,b,c均不为零,因为题中没有指明a,b,c的正负,故应该分四种情况:(1)当a,b,c均大于零时;(2)当a,b,c均小于零时;(3)当a,b,c中有两个大于零,一个小于零时;(4)当a,b,c中有两个小于零,一个大于零时,从而确定答案.
解答 解:∵abc≠0,
∴a≠0,b≠0,c≠0.
∵(1)当a,b,c均大于零时,原式=3;
(2)当a,b,c均小于零时,原式=-3;
(3)当a,b,c中有两个大于零,一个小于零时,原式=1;
(4)当a,b,c中有两个小于零,一个大于零时,原式=-1.
∴$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$的所有可能值是:±3,±1.
点评 此题主要考查了绝对值的性质,采用分类讨论思想是解答此题的关键.

练习册系列答案
相关题目
10.若|a-2|+|b+3|=0,则a-b-1的值为( )
| A. | 4 | B. | -6 | C. | 5 | D. | -7 |
 已知矩形ABCD的面积为10$\sqrt{6}$,求图中阴影部分的面积.
已知矩形ABCD的面积为10$\sqrt{6}$,求图中阴影部分的面积.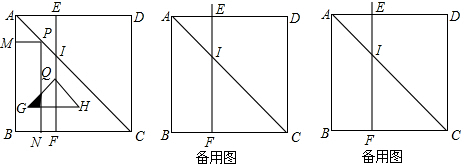
 如图,将△ABC的一角向内折叠,使点C落在△ABC内,已知∠1=30°,∠C=40°,求∠2的度数.
如图,将△ABC的一角向内折叠,使点C落在△ABC内,已知∠1=30°,∠C=40°,求∠2的度数.