题目内容
1.如图,在正方形ABCD中,AB=6,E为AD上一点,EF⊥BC交BC于点F,BF=2.点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿AC方向运动,点Q从点F出发以每秒2个单位长度的速度沿射线FE方向运动,P、Q两点同时出发,当点P到达点C时停止运动,点Q也随之停止.过点P作PM⊥AB于点M,PN⊥BC于点N,得到矩形PMBN.以点Q为直角顶点向下作等腰Rt△QGH,且斜边GH∥BC,GH=QF.设运动时间为t(单位:秒).(1)当t=1时,点G落在PN线段上;当t=2时,GH=PN;
(2)当△QGH和矩形PMBN有重叠部分时,求重叠(阴影)部分图形面积S与t的函数关系式,并求出自变量的取值范围;
(3)在P、Q两点的运动过程中,是否存在某一时刻使△MPQ为等腰三角形?若存在,请直接写出运动时间t的值;若不存在,请说明理由.
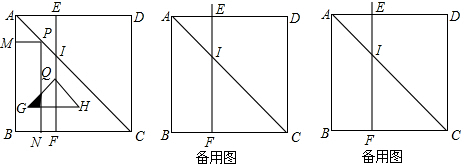
分析 (1)点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿AC方向运动,则P每秒1个单位长度的速度向右(下)运动,据此即可求解;
(2)求出G到达AB,和PQ重合时t的值,则可以分成不同情况进行讨论,根据阴影部分的面积可以化成几个直角三角形的面积的和、差即可求解;
(3)根据(2)中分成的情况,分情况进行讨论,从而列方程求解.
解答  解:(1)∵点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿AC方向运动,
解:(1)∵点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿AC方向运动,
∴P每秒1个单位长度的速度向右运动,
∵GH=QF=2t,
∴GK=t,
则点G落在PN线段上时,t+t=2,
解得:t=1;
PN=$\frac{\sqrt{2}}{2}$PC=$\frac{\sqrt{2}}{2}$(6$\sqrt{2}$-$\sqrt{2}$t)=6-t.
则当6-t=2t,即t=2时,GH=PH.
故答案是:1,2;
(2)当t=2时,P移动到EF上,此时P.H和Q重合.
则当1<t≤2时,如图1,重合部分是等腰直角三角形,则GW=t+t-2=2t-2,
S=$\frac{1}{2}$(2t-2)2,即S=2(t-1)2;
当2<t≤$\frac{8}{3}$时,如图2,
S△QTH=$\frac{1}{2}$×2t•t=t2,
GK=t-2,则S△GRT=$\frac{1}{2}$(t-2)2;
JH=2t-2-(t-2)=t,则S△HJY=$\frac{1}{2}$t2;
S△QSZ=$\frac{1}{2}$(3t-6)2=$\frac{9}{2}$(t-2)2,
PZ=t-2-(3t-6)=4-2t,
则S△PZY=$\frac{1}{2}$(4-2t)2=2(2-t)2,
则S=t2-$\frac{1}{2}$(t-2)2-$\frac{1}{2}$t2-2(2-t)2=10t-10;
当$\frac{8}{3}$<t<3时,如图3.
(3)在图1中,即当1<t≤2时,若△MPQ是等腰三角形,则有PM=PQ,
PM=t,PQ=$\sqrt{(2-t)^{2}+(6-t-2t)^{2}}$=$\sqrt{10}$(2-t),
则t=$\sqrt{10}$(2-t),解得t=$\frac{10-\sqrt{10}}{3}$;
当2<t<3,不能构成等腰三角形.
总之,t=$\frac{10-\sqrt{10}}{3}$
点评 本题考查了图形的移动,注意到点P从点A出发以每秒$\sqrt{2}$个单位长度的速度沿AC方向运动,则P每秒1个单位长度的速度向右(下)运动,正确进行讨论是关键.

 名校课堂系列答案
名校课堂系列答案
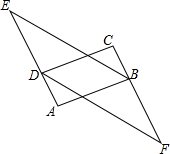 如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.
如图,四边形ABCD中,AB=DC,AB∥DC,延长AD到E,延长CB到F,使DE=BF,猜想BE与DF的关系,并证明你的结论.