题目内容
 如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.求证:EF是⊙O的切线.
如图,AB是⊙O的直径,AC是弦,直线EF经过点C,AD⊥EF于点D,∠DAC=∠BAC.求证:EF是⊙O的切线.考点:切线的判定
专题:证明题
分析:连接OC,由OA=OC得∠OAC=∠OCA,而∠DAC=∠BAC,则∠OCA=∠DAC,根据平行线的判定定理得OC∥AD,由于AD⊥EF,根据平行线的性质得OC⊥CF,然后根据切线的判定定理即可得到EF是⊙O的切线.
解答:证明 :连接OC,如图,
:连接OC,如图,
∵OA=OC,
∴∠OAC=∠OCA,
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥EF,
∴OC⊥CF,
∴EF是⊙O的切线.
 :连接OC,如图,
:连接OC,如图,∵OA=OC,
∴∠OAC=∠OCA,
∵∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AD⊥EF,
∴OC⊥CF,
∴EF是⊙O的切线.
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了平行线的判定与性质.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
计算-32×
的值是( )
| (-2)2 |
| 3 |
A、-
| ||
B、-
| ||
| C、12 | ||
| D、-12 |
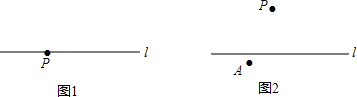 我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢?
我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢? 如图,边长为4的菱形ABCD的内角∠B=60°,O是对角线AC的中点.E、F、G、H 分别在菱形ABCD的四条边上,四边形EBOF与四边形HDOG关于直线AC对称,且∠EOF=60°.
如图,边长为4的菱形ABCD的内角∠B=60°,O是对角线AC的中点.E、F、G、H 分别在菱形ABCD的四条边上,四边形EBOF与四边形HDOG关于直线AC对称,且∠EOF=60°.