题目内容
1.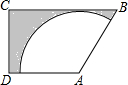 如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在梯形内画出一个最大的扇形,则阴影部分的面积为10$\sqrt{3}$-4π.
如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=4,BC=6,以点A为圆心在梯形内画出一个最大的扇形,则阴影部分的面积为10$\sqrt{3}$-4π.
分析 设扇形与BC相切于点E,连接AE,首先证明四边形CDAE是矩形,在RT△AEB中求出AE以及∠EAB,求出圆心角∠DAB,根据S阴=S梯形ABCD-${S}_{扇形}\\;\$即可解决问题.
解答 解:如图设扇形与BC相切于点E,连接AE,则AE⊥BC.
∵AD∥BC,∠C=90°,
∴∠D=∠C=∠AEC=90°,
∴四边形ADCE是矩形,
∴AD=CE=4,
∵BC=6,
∴BE=2,
在RT△AEB中,∵∠AEB=90°,AB=4,EB=2,
∴AE=$\sqrt{A{B}^{2}-E{B}^{2}}$=2$\sqrt{3}$,AB=2EB,
∴∠EAB=30°,
∵∠DAE=90°,
∴∠DAB=120°,
∴S阴=S梯形ABCD-${S}_{扇形}\\;\$=$\frac{1}{2}$(4+6)$•2\sqrt{3}$-$\frac{120π•(2\sqrt{3})^{2}}{360}$=10$\sqrt{3}$-4π.
故答案为10$\sqrt{3}$-4π
点评 本题考查扇形的面积的计算、梯形面积的计算等知识,解题的关键是添加辅助线,构造特殊四边形以及直角三角形,记住扇形面积公式S扇形=$\frac{nπ{R}^{2}}{360}$=$\frac{1}{2}$LR(n是圆心角,R是半径,L是弧长),属于中考常考题型.

练习册系列答案
相关题目
6.已知点M(m,n)在直线y=x+3上,则代数式m2-2mn+n2的值为( )
| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
13.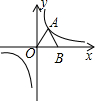 如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )
如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )
 如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )
如图,等边△OAB的边长为2,点B在x轴上,点A在双曲线y=$\frac{k}{x}$(k≠0)上,将△OAB绕点O顺时针旋转α度(0<α<360°),使点A仍落在双曲线y=$\frac{k}{x}$(k≠0)上,则α的值不可能是( )| A. | 30 | B. | 180 | C. | 200 | D. | 210 |
10.下列计算中,正确的是( )
| A. | a0=1 | B. | $\sqrt{(-3)^{2}}$=-3 | C. | m6÷m2=m3 | D. | 3-2=$\frac{1}{9}$ |
 如图所示,△ABC中,E,F分别是边AB,AC上的点,且满足$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$,则△AEF与
如图所示,△ABC中,E,F分别是边AB,AC上的点,且满足$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$,则△AEF与 在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(-3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx-5k(k≠0),BC=OB.
在平面直角坐标系xOy中,抛物线y=ax2+bx经过点A(-3,4),直线l与x轴相交于点B,与∠AOB的平分线相交于点C,直线l的解析式为y=kx-5k(k≠0),BC=OB. 如图,已知直线y=3x-3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.
如图,已知直线y=3x-3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点,该抛物线的对称轴与x轴交于点E.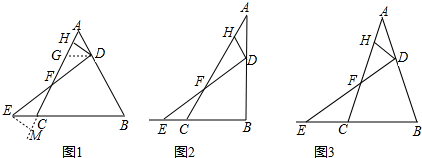
 如图,在?ABCD中,DB=DC,∠A=67°,CE⊥BD于点E,则∠BCE=23°.
如图,在?ABCD中,DB=DC,∠A=67°,CE⊥BD于点E,则∠BCE=23°.