题目内容
10．
如图所示，△ABC中，E，F分别是边AB，AC上的点，且满足$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$，则△AEF与△ABC的面积比是1：9．
分析 由已知条件易证△AEF∽△ABC，根据相似三角形的性质即可求出△AEF与△ABC的面积比．
解答 解：
∵$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$，
∴$\frac{AE}{AB}=\frac{AF}{AC}=\frac{1}{3}$，
又∵∠A=∠A，
∴△AEF∽△ABC，
∴△AEF与△ABC的面积比=1：9，
故答案为：1：9．
点评 本题考查了相似三角形的判定和性质，熟悉相似三角形的性质：相似三角形的面积比是相似比的平方是解题关键．
练习册系列答案
相关题目
如图，△ABC是⊙O的内接正三角形，⊙O的半径为3，则图中阴影部分的面积是3π．
如图，在?ABCD中，AB=2$\sqrt{13}$cm，AD=4cm，AC⊥BC，则△DBC比△ABC的周长长4cm．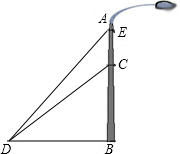
如图，一垂直于地面的灯柱AB被一钢线CD固定，CD与地面成45°夹角（∠CDB=45°），在C点上方2米处加固另一条钢线ED，ED与地面成53°夹角（∠EDB=53°），那么钢线ED的长度约为多少米？（结果精确到1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）
15．下面四个几何体中，其主视图不是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
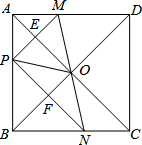如图，在正方形ABCD中，点P是AB上一动点（不与A，B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N．下列结论：
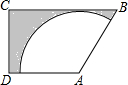如图，梯形ABCD中，AD∥BC，∠C=90°，AB=AD=4，BC=6，以点A为圆心在梯形内画出一个最大的扇形，则阴影部分的面积为10$\sqrt{3}$-4π．