题目内容
当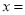 ______时,
______时,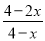 的值与
的值与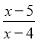 的值相等.
的值相等.
 -1
【解析】本题主要考查了解分式方程. 由题意可得分式方程 =,方程两边同乘以(4-x),去分母,化为整式方程求解.
【解析】
由题意可得分式方程:
=,
方程两边同乘以(4-x),
得4-2x=5-x,
整理得x=-1,
经检验,原方程的解为x=-1.
-1
【解析】本题主要考查了解分式方程. 由题意可得分式方程 =,方程两边同乘以(4-x),去分母,化为整式方程求解.
【解析】
由题意可得分式方程:
=,
方程两边同乘以(4-x),
得4-2x=5-x,
整理得x=-1,
经检验,原方程的解为x=-1.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
已知抛物线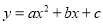 (a<0)过A(-2,0)、O(0,0)、B(-3,
(a<0)过A(-2,0)、O(0,0)、B(-3, 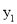 )、C(3,
)、C(3, 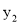 )四点,则
)四点,则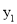 与
与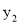 的大小关系是__________
的大小关系是__________
 【解析】由已知得抛物线与x轴交于A(-2,0)、O(0,0)两点,开口向下,对称轴为x==-1,可知B(-3, )、C(3, )两点在对称轴的两边,点B离对称轴较近,再根据抛物线图象可得.
故答案为: .
【解析】由已知得抛物线与x轴交于A(-2,0)、O(0,0)两点,开口向下,对称轴为x==-1,可知B(-3, )、C(3, )两点在对称轴的两边,点B离对称轴较近,再根据抛物线图象可得.
故答案为: . 如图,已知抛物线y=﹣x2+bx+c的对称轴为直线x=1,且与x轴的一个交点为(3,0),那么它对应的函数解析式是 .
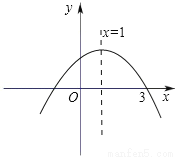
 y=﹣x2+2x+3
【解析】
试题分析:∵抛物线y=﹣x2+bx+c的对称轴为直线x=1,
∴=1,解得b=2,
∵与x轴的一个交点为(3,0),
∴0=﹣9+6+c,
解得c=3,
故函数解析式为y=﹣x2+2x+3.
故答案为:y=﹣x2+2x+3
y=﹣x2+2x+3
【解析】
试题分析:∵抛物线y=﹣x2+bx+c的对称轴为直线x=1,
∴=1,解得b=2,
∵与x轴的一个交点为(3,0),
∴0=﹣9+6+c,
解得c=3,
故函数解析式为y=﹣x2+2x+3.
故答案为:y=﹣x2+2x+3 某厂原计划在规定时间内生产通讯设备60台,由于改进了操作技术,每天生产的 台数比原计划多50%,结果提前两天完成任务.求改进操作技术后每天生产通讯设备多少台.
 15台.
【解析】试题分析:设改进操作技术前每天生产通讯设备x台,则改进操作技术后每天生产通讯设备1.5x台,根据提前两天完成任务,列方程求解即可.
试题解析:设改进技术前每天生产x台,根据题意,得,解得x=10,
经检验x=10是原方程的解,
则1.5x=15,
所以改进操作技术后每天生产通讯设备15台.
15台.
【解析】试题分析:设改进操作技术前每天生产通讯设备x台,则改进操作技术后每天生产通讯设备1.5x台,根据提前两天完成任务,列方程求解即可.
试题解析:设改进技术前每天生产x台,根据题意,得,解得x=10,
经检验x=10是原方程的解,
则1.5x=15,
所以改进操作技术后每天生产通讯设备15台. 若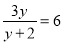 ,则
,则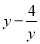 =_______.
=_______.
 -3
【解析】解方程,得:y=-4,经检验y=-4是方程的解,
所以=-4+1=-3,
故答案为:-3.
-3
【解析】解方程,得:y=-4,经检验y=-4是方程的解,
所以=-4+1=-3,
故答案为:-3. 下列关于x的方程中,不是分式方程的是( )
A. 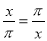 B.
B. 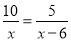 C.
C. 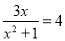 D.
D. 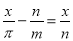
 D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D.
D
【解析】A、分母中含有未知数,是分式方程,故本选项不符合题意;
B、分母中含有未知数,是分式方程,故本选项不符合题意;
C、分母中含有未知数,是分式方程,故本选项不符合题意;
D、分母中不含有未知数,不是分式方程,故本选项符合题意,
故选D. 已知抛物线y=ax2+b x+c经过A,B,C三点,当x≥0时,其图象如图所示.
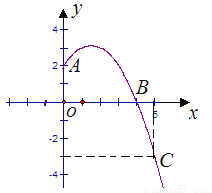
(1)求抛物线的解析式,写出抛物线的顶点坐标;
(2)画出抛物线y=ax2+b x+c当x<0时的图象;
(3)利用抛物线y=ax2+b x+c,写出x为何值时,y>0.
 (1)抛物线y =顶点(,)(2)略(3) 当-1<x<4时, y >0
【解析】试题分析:本题的关键是求出抛物线的解析式,在题目给出的图象中可得出A、B、C三点的坐标,可用待定系数求出抛物线的解析式,进而可画出x<0时抛物线的图象,以及y>0时x的取值范围.
【解析】
(1)由图象,可知A(0,2),B(4,0),C(5,﹣3),
得方程组.
解得a=﹣,b=,c=2....
(1)抛物线y =顶点(,)(2)略(3) 当-1<x<4时, y >0
【解析】试题分析:本题的关键是求出抛物线的解析式,在题目给出的图象中可得出A、B、C三点的坐标,可用待定系数求出抛物线的解析式,进而可画出x<0时抛物线的图象,以及y>0时x的取值范围.
【解析】
(1)由图象,可知A(0,2),B(4,0),C(5,﹣3),
得方程组.
解得a=﹣,b=,c=2.... 平行四边形ABCD的周长32,5AB=3BC,则对角线AC的取值范围为( )
A.6<AC<10 B.6<AC<16 C.10<AC<16 D.4<AC<16
 D.
【解析】
试题分析:∵平行四边形ABCD的周长32,5AB=3BC,∴2(AB+BC)=2(BC+BC)=32,
∴BC=10,∴AB=6,∴BC﹣AB<AC<BC+AB,即4<AC<16.
故选D.
D.
【解析】
试题分析:∵平行四边形ABCD的周长32,5AB=3BC,∴2(AB+BC)=2(BC+BC)=32,
∴BC=10,∴AB=6,∴BC﹣AB<AC<BC+AB,即4<AC<16.
故选D. 
