题目内容
11.先化简,再求值:(x-2+$\frac{3}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$,其中x=(π-2015)0-$\sqrt{4}$+($\frac{1}{3}$)-1.分析 先通分,然后进行四则运算,最后将x的值求出来,再代入计算即可.
解答 解:原式=$[\frac{(x-2)(x+2)}{x+2}+\frac{3}{x+2}]•\frac{x+2}{{(x+1)}^{2}}$
=$\frac{{x}^{2}-4+3}{x+2}•\frac{x+2}{{(x+1)}^{2}}$
=$\frac{(x+1)(x-1)}{x+2}•\frac{x+2}{{(x+1)}^{2}}$
=$\frac{x-1}{x+1}$
$x={(π-2015)}^{0}-\sqrt{4}+{(\frac{1}{3})}^{-1}$=1-2+3=2,
当x=2时,原式=$\frac{2-1}{2+1}=\frac{1}{3}$.
点评 本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
6.下列运算正确的是( )
| A. | 5m+2m=7m2 | B. | -2m2•m3=2m5 | C. | (-a2b)3=-a6b3 | D. | (b+2a)(2a-b)=b2-4a2 |
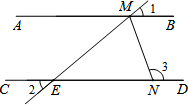 如图,∠1=∠2=40°,MN平分∠EMB,则∠3=110°.
如图,∠1=∠2=40°,MN平分∠EMB,则∠3=110°.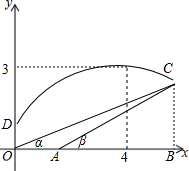 某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.
某防空部队进行射击训练,在地面上设有O、A两个观测点,测得空中固定目标C的仰角分别为α、β,OA=1千米,已知tanα=$\frac{9}{28}$,tanβ=$\frac{3}{8}$.一直升飞机在O点正上方$\frac{5}{3}$千米D点处,向目标C发射防空导弹,导弹飞行的轨道近似为抛物线,当导弹飞行到距O点水平距离4千米时,达到最大高度3千米.建立如图所示的平面直角坐标系.