题目内容
11.如图,等边△ABC的边长为8,动点M从点B出发,沿B→A→C→B的方向以3cm/s的速度运动,动点N从点C出发,沿C→A→B→C方向以2cm/s的速度运动.(1)若动点M、N同时出发,经过几秒钟两点第一次相遇?
(2)若动点M、N同时出发,且其中一点到达终点时,另一点即停止运动.那么运动到第几秒钟时,点A、M、N以及△ABC的边上一点D恰能构成一个平行四边形?求出时间t并请指出此时点D的具体位置.
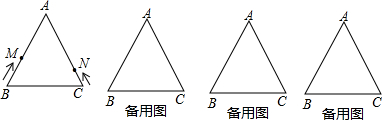
分析 (1)设经过t秒钟两点第一次相遇,然后根据点M运动的路程+点N运动的路程=AB+CA列方程求解即可;
(2)首先根据题意画出图形:如图①,当0≤t≤$\frac{8}{3}$时,MC+BN=AN+BN=8;当$\frac{8}{3}$<t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;4<t$≤\frac{16}{3}$时,MB+NC=AN+CN=8;当$\frac{16}{3}$<t≤8时,△BNM为等边三角形,由BN=BM可求得t的值.
解答 解:(1)由题意得:3t+2t=16,解得:t=$\frac{16}{5}$;
(2)①当0≤t≤$\frac{8}{3}$时,点M、N、D的位置如图1所示: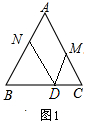
∵四边形ANDM为平行四边形,
∴DM=AN,DM∥AN.
∴∠MDC=∠ABC=60°
∵△ABC为等腰三角形,
∴∠C=60°.
∴∠MDC=∠C.
∴MD=MC
∴MC+BN=AN+BN=8,即:3t+2t=8,t=$\frac{8}{5}$,
此时点D在BC上,且BD=$\frac{24}{5}$(或CD=$\frac{16}{5}$),
②当$\frac{8}{3}$<t≤4时,此时A、M、N三点在同一直线上,不能构成平行四边形;
③4<t$≤\frac{16}{3}$时,点M、N、D的位置如图所2示: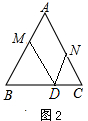
∵四边形ANDM为平行四边形,
∴DN=AM,AM∥DN.
∴∠MDB=∠ACB=60°
∵△ABC为等腰三角形,
∴∠B=60°.
∴∠MDB=∠B.
∴MD=MB.
∴MB+NC=AN+CN=8,3t-8+2t-8=8,解得:t=$\frac{24}{5}$,
此时点D在BC上,且BD=$\frac{32}{5}$(或CD=$\frac{8}{5}$),
④当$\frac{16}{3}$<t≤8时,点M、N、D的位置如图所3示: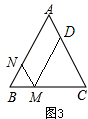
则BN=16-2t,BM=24-3t,
由题意可知:△BNM为等边三角形,
∴BN=BM,即:2t-8=3t-16,解得t=8,此时M、N重合,不能构成平行四边形.
答:运动了$\frac{8}{5}$或$\frac{24}{5}$时,A、M、N、D四点能够成平行四边形,此时点D在BC上,且BD=$\frac{24}{5}$或$\frac{32}{5}$.
点评 本题主要考查的是平行四边形的性质和等边三角形的性质,利用平行四边形的性质和等边三角形的性质求得相关线段的长度,然后列方程求解是解题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 25% | B. | 50% | C. | 75% | D. | 85% |
| A. | 17.58×103 | B. | 175.8×104 | C. | 1.758×105 | D. | 1.758×104 |
| A. | 2 | B. | -1 | C. | 1 | D. | 0 |
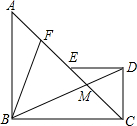 如图,等腰Rt△ABC与等腰RtCDE斜边AC与CE共线,连接BD交AC于M,F为AE中点,连接BF.
如图,等腰Rt△ABC与等腰RtCDE斜边AC与CE共线,连接BD交AC于M,F为AE中点,连接BF. 已知在Rt△ABC中,∠B=90°,线段AE、CD分别平分∠BAC、∠ACB,则∠APD的度数为45°.
已知在Rt△ABC中,∠B=90°,线段AE、CD分别平分∠BAC、∠ACB,则∠APD的度数为45°.