题目内容
16. 已知如图,在等边三角形ABC中,若剪去∠B,则图中∠α+∠β等于( )
已知如图,在等边三角形ABC中,若剪去∠B,则图中∠α+∠β等于( )| A. | 240° | B. | 320° | C. | 180° | D. | 无法计算 |
分析 根据等边三角形的性质及四边形内角和定理进行解答.
解答 解:∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,
∵四边形的内角和是360°,
∴∠α+∠β=360°-∠A-∠C=360°-60°-60°=240°.
故选A.
点评 本题考查的是等边三角形的性质及四边形内角和定理,熟知等边三角形的性质是解答此题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7. 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )
 如图,下列条件中,不能证明△ABC≌△DCB的是( )
如图,下列条件中,不能证明△ABC≌△DCB的是( )| A. | AB=CD,AC=BD | B. | AB=CD,∠ABC=∠BCD | C. | ∠ABC=∠DCB,∠A=∠D | D. | AB=CD,∠A=∠D |
11.下列各组数可能是一个三角形边长的是( )
| A. | 1,2,3 | B. | 2,3,4 | C. | 3,4,9 | D. | 5,5,12 |
1.下列函数中,能表示y是x的反比例函数的是( )
| A. | y=$\frac{1}{2x}$ | B. | y=$\frac{1}{x-1}$ | C. | y=2x | D. | y=$\frac{2}{\sqrt{x}}$ |
 甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题:
甲驾车从A地去往B地,到达后停留3个小时,然后返回,往返车速都为120千米/时,乙驾车从B地去往A地,到达后停留1.5小时,因事提前返回,乙往返的车速不变,如图是两车距A地的路程s(千米0与行驶时间t(小时)之间的函数图象,请结合图象回答下列问题: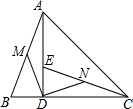 如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.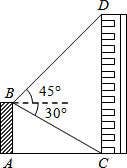 如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为32.4m.($\sqrt{3}$≈1.7)
如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,则楼房CD的高度为32.4m.($\sqrt{3}$≈1.7) 如图,在平面直角坐标中,已知四边形ABCD是正方形,点A在原点,点B的坐标是(3,1),则点D的坐标是(-1,3).
如图,在平面直角坐标中,已知四边形ABCD是正方形,点A在原点,点B的坐标是(3,1),则点D的坐标是(-1,3).