题目内容
2.如图1,在矩形ABCD中,AB=6cm,AD=8cm,点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ⊥BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3m/s,以O为圆心,0.8cm为半径作⊙O,点P与点O同时出发,设它们的运动时间为t(单位:s)(0<t<$\frac{8}{5}$).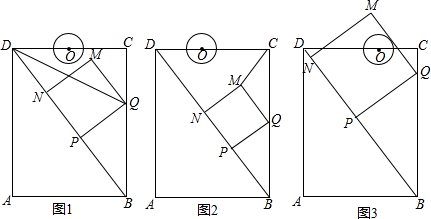
发现:
(1)BD=10;
(2)当t=$\frac{1}{2}$时,正方形PQMN的边长为$\frac{3}{2}$;
思考:如图2,连接DQ平分∠BDC时,t的值为1;
探究:如图3,在运动过程中,当QM与⊙O相切时,求t的值.
分析 发现:(1)利用勾股定理BD=$\sqrt{A{D}^{2}+A{B}^{2}}$即可解决问题.
(2)当t=$\frac{1}{2}$时,BP=2,由△PBQ∽△CBD,推出$\frac{PB}{BC}$=$\frac{PQ}{CD}$,即可解决问题.
思考:如图1中,由DQ平分∠BDC,QP⊥DB,QC⊥DC,推出QP=QC由(1)可知,△PBQ∽△CBD,推出$\frac{PB}{BC}$=$\frac{PQ}{DC}$=$\frac{BQ}{BD}$,列出方程即可解决问题.
探究:如图2中,令⊙O与直线QM相切于点H,QM与CD交于点E.由△OHE∽△BCD,可得$\frac{OH}{BC}$=$\frac{OE}{BD}$,列出方程即可解决问题.
解答 解:发现:(1)如图12-1,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD=6.AD=BC=8,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
故答案为10.
(2)如图1中,当t=$\frac{1}{2}$时,BP=2,
∵PQ⊥BD,∴∠BPQ=∠C=90°,
∵∠PBQ=∠DBC,
∴△PBQ∽△CBD,
∴$\frac{PB}{BC}$=$\frac{PQ}{CD}$,即$\frac{2}{8}$=$\frac{PQ}{6}$,
∴PQ=$\frac{3}{2}$,即正方形PQMN的边长为$\frac{3}{2}$.
故答案为$\frac{3}{2}$.
思考:如图1中,∵DQ平分∠BDC,QP⊥DB,QC⊥DC,
∴QP=QC,
由(1)可知,△PBQ∽△CBD,
∴$\frac{PB}{BC}$=$\frac{PQ}{DC}$=$\frac{BQ}{BD}$,
∴$\frac{4t}{8}$=$\frac{PQ}{6}$=$\frac{BQ}{10}$,
∴PQ=3t,BQ=5t,
∴3t=8-5t,
∴t=1.
故答案为1.
探究:如图,令⊙O与直线QM相切于点H,QM与CD交于点E.
∵EC=$\frac{3}{4}$(8-5t),DO=3t,
∴OE=6-3t-$\frac{3}{4}$(8-5t)=$\frac{3}{4}$t,
∵OH⊥MQ,∴∠OHE=90°,
∵∠HEO=∠CEQ,∴∠HOE=∠CQE=∠CBD,
∵∠OHE=∠C=90°,∴△OHE∽△BCD,
∴$\frac{OH}{BC}$=$\frac{OE}{BD}$,
∴$\frac{0.8}{8}$=$\frac{\frac{3}{4}t}{10}$,
∴t=$\frac{4}{3}$,即当t=$\frac{4}{3}$s时,⊙O与直线QM相切.
点评 本题考查圆综合题、相似三角形的判定和性质、勾股定理、角平分线性质定理等知识,解题的关键是灵活运用所学知识,正确寻找相似三角形,学会用方程的思想思考问题,属于中考压轴题.

| A. | -3.567 | B. | 0.101001 | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
| A. | 扩大为原来的2倍 | B. | 缩小为原来的$\frac{1}{2}$ | C. | 扩大为原来的4倍 | D. | 缩小为原来的$\frac{1}{4}$ |
 根据下列语句画出图形.
根据下列语句画出图形.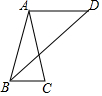 如图,已知AB=AC=AD,且∠C=2∠D,求证AD∥BC.
如图,已知AB=AC=AD,且∠C=2∠D,求证AD∥BC.