题目内容
18．
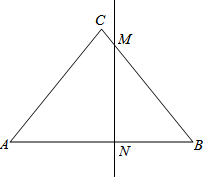如图，已知△ABC，∠C=90°，AB的垂直平分线交BC于点M，交AB于于点N．若AC=$\sqrt{3}$，MB=2MC，求AB的长．
分析 连接MA，可求得MA=2MC，在Rt△AMC中可求得MC，则可求BC，在Rt△ABC中，由勾股定理可求得AB．
解答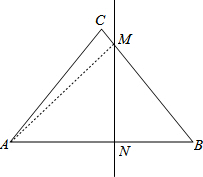 
解：如图，连接MA，
∵M在线段AB的垂直平分线上，
∴MA=MB=2MC，
∵∠C=90°，
∴AC2+CM2=MA2，即3+MC2=4MC2，
解得MC=1，
∴MB=2MC=2，
∴BC=3，
在Rt△ABC中，由勾股定理可得AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{3+9}$=2$\sqrt{3}$，
即AB的长为2$\sqrt{3}$．
点评 本题主要考查线段垂直平分线的性质，掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键．
练习册系列答案
相关题目
如图，AB∥DE，若∠1=45°，则∠2=135°．
如图，P是⊙O外一点，A、B、C是⊙O上的三点，∠AOB=60°，PA、PB分别交$\widehat{ACB}$于M、N两点，则∠APB的范围是0°＜∠APB＜30°．