题目内容
10.化简:$\sqrt{x+\sqrt{2x-3}-1}$+$\sqrt{x-\sqrt{2x-3}-1}$(其中:$\frac{3}{2}$≤x≤2)的结果等于$\sqrt{2}$.分析 直接利用完全平方公式化简,再利用二次根式的性质求出即可.
解答 解:设t=$\sqrt{x+\sqrt{2x-3}-1}$+$\sqrt{x-\sqrt{2x-3}-1}$,
则t2=x+$\sqrt{2x-3}$-1+x-$\sqrt{2x-3}$-1+2$\sqrt{(x+\sqrt{2x-3}-1)(x-\sqrt{2x-3}-1)}$
=2x-2+2$\sqrt{(x-2)^{2}}$
=2x-2+2(2-x)
=2,
解得:t=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 此题主要考查了二次根式的化简求值,正确应用换元法求出是解题关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
1.分式方程$\frac{1}{x(x-2)}$=$\frac{1}{2-x}$的根为( )
| A. | x1=2,x2=-1 | B. | x=-1 | C. | x=2 | D. | x1=2,x2=1 |
20.下列计算正确的是( )
| A. | a4+a4=a8 | B. | a3•a2=a5 | C. | a8÷a2=a4 | D. | (a3)4=a7 |
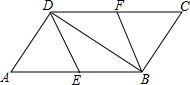 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.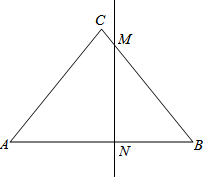 如图,已知△ABC,∠C=90°,AB的垂直平分线交BC于点M,交AB于于点N.若AC=$\sqrt{3}$,MB=2MC,求AB的长.
如图,已知△ABC,∠C=90°,AB的垂直平分线交BC于点M,交AB于于点N.若AC=$\sqrt{3}$,MB=2MC,求AB的长.