题目内容
15. 矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根
矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根(1)求k的取值范围;
(2)矩形对角线的长能否为$\frac{\sqrt{14}}{2}$?请说明理由;
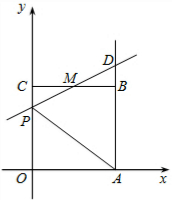
(3)当OABC为正方形时,将其放置在如图所示的直角坐标系中,点A在x轴的正半轴上,点C在y轴的正半轴上,M是BC的中点,P(0,m)是线段OC上一动点(C点除外),直线PM交AB的延长线于点D.当△APD是等腰三角形时,求m的值.
分析 (1)根据根的判别式,可得答案;
(2)根据根与系数的关系及勾股定理,可得关于k的方程,根据解方程,可得答案;
(3)分类讨论:当PA=PD时,当PA=PD时,当PD=AD时,根据勾股定理,可得关于m的方程,根据解方程,可得答案.
解答 解:(1)由矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根,得
△=(k+1)2-4($\frac{1}{4}$k2+$\frac{7}{4}$)>0,
解得k>3;
(2)矩形对角线的长不能为$\frac{\sqrt{14}}{2}$,理由如下:
a+b=k+1,ab=$\frac{1}{4}$k2+$\frac{7}{4}$,
a2+b2=(a+b)2-2ab=(k+1)2-2($\frac{1}{4}$k2+$\frac{7}{4}$)=($\frac{\sqrt{14}}{2}$)2,
化简,得
k2+4k-12=0.
解得k1=2,k2=-6,
∵k>3,
∴矩形对角线的长不能为$\frac{\sqrt{14}}{2}$;
(3)当OABC为正方形时,k=3,
原方程为x2-4x+4=0,
解得x1=x2=2,
∴OA=AB=BC=OC=2,CM=BM=1.
①当PA=PD时,OP=m,PC=2-m,CM=BM=1,
PA2=OP2+OA2=m2+22,PD2=(2PM)2=4(PM2)=4(PC2+CM2)=4(2-m)2+4,
∴m2+4=4(2-m)2+4,
解得m1=$\frac{4}{3}$,m2=4;
②当PA=PD时,BD=PC=2-m,AD=AB+BD=4-m,
PA2=PD2,
即m2+22=(4-m)2,
解得m3=$\frac{3}{2}$;
③当PD=AD时,4(2-m)2+4=(4-m)2,
解得m4=$\frac{8}{3}$,m5=0,
综上所述:m1=$\frac{4}{3}$,m2=4,m3=$\frac{3}{2}$,m4=$\frac{8}{3}$,m5=0.
点评 本题考查了一次函数综合题,利用了根的判别式;利用根与系数的关系及勾股定理得出关于k的方程是解题关键;利用勾股定理的出关于m的方程是解题关键,要分类讨论,以防遗漏.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案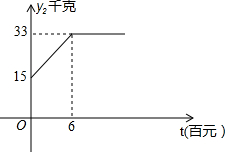 茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).
茶农张大爷种有茶树共50亩,其中丘陵地20亩,山地30亩,每亩丘陵地产量y1(千克)与每亩投资x(百元)之间的函数关系式为:y1=$\left\{{\begin{array}{l}{-\frac{1}{4}{(x-8)}^2+36(0≤x≤6)}\\{35(x>6)}\end{array}}\right.$;每亩山地产量y2(千克)与每亩投资x(百元)之间的关系如图所示,张大爷现在总投资金240(百元).(1)试求张大爷每亩丘陵地投资600元和每亩山地投资600元时茶叶的总产量分别是多少千克?
(2)写出张大爷家茶叶总产量W (千克)与丘陵地每亩投资x(百元)之间的函数关系式,并指出x的取值范围;
(3)当x取何值时,茶叶的总产量最高?最高产量为多少千克?
(4)在(2)的条件下,如果其中700千克为毛尖茶.其余为龙井茶.现在由乡政府统一组织向外销售,且包装要求及价格如表:
| 型号 | A型包装 | B型包装 | C型包装 |
| 每盒装 | 龙井1千克 | 毛尖1千克 | 毛尖0.4千克;龙井0.6千克 |
| 每盒价格 | 45元 | 60元 | 56元 |
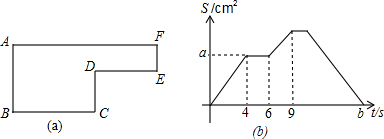
| A. | 图(a)中的BC长是4cm | B. | 图(b)中的a是12 | ||
| C. | 图(a)中的图形面积是60cm2 | D. | 图(b)中的b是19 |
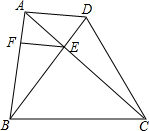 如图,已知在梯形ABCD中,AD∥BC,AC与BD交于点E,作EF∥BC交AB于点F,BC=CD,EF=ED.求证:△BCD是等边三角形.
如图,已知在梯形ABCD中,AD∥BC,AC与BD交于点E,作EF∥BC交AB于点F,BC=CD,EF=ED.求证:△BCD是等边三角形. 如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.
如图,已知点D、E、F分别在△ABC的边AB、AC、BC上,DE∥BC、DF∥AC,AE=6,EC=8,求BF:FC的值.