题目内容
20.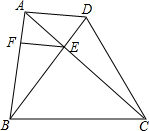 如图,已知在梯形ABCD中,AD∥BC,AC与BD交于点E,作EF∥BC交AB于点F,BC=CD,EF=ED.求证:△BCD是等边三角形.
如图,已知在梯形ABCD中,AD∥BC,AC与BD交于点E,作EF∥BC交AB于点F,BC=CD,EF=ED.求证:△BCD是等边三角形.
分析 由AD∥BC可判断△ADE∽△CBE,则由相似的性质得$\frac{AD}{BC}$=$\frac{DE}{BE}$,再证明△BEF∽△BDA得到$\frac{EF}{AD}$=$\frac{BE}{BD}$,由比例性质得$\frac{EF}{BE}$=$\frac{AD}{BD}$,而EF=ED,所以$\frac{AD}{BD}$=$\frac{AD}{BC}$,即有BD=BC,再加上BC=CD,于是根据等边三角形的判定方法即可得到结论.
解答 证明:∵AD∥BC,
∴△ADE∽△CBE,
∴$\frac{AD}{BC}$=$\frac{DE}{BE}$,
∵EF∥BC,
∴EF∥AD,
∴△BEF∽△BDA,
∴$\frac{EF}{AD}$=$\frac{BE}{BD}$,
∴$\frac{EF}{BE}$=$\frac{AD}{BD}$,
∵EF=ED,
∴$\frac{ED}{BE}$=$\frac{AD}{BD}$,
∴$\frac{AD}{BD}$=$\frac{AD}{BC}$,
∴BD=BC,
∴BC=CD,
∴BD=BC=CD,
∴△BCD是等边三角形.
点评 本题考查了相似三角形的判定与性质:三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是利用平行线构造相似三角形,然后利用相似三角形的性质进行计算和判断线段之间的关系.也考查了等边三角形的判定.

练习册系列答案
相关题目
8.如图,在一张矩形纸片的一端,将折出的一个正方形展平后,又折成了两个相等的矩形,再把纸片展平,折出小矩形的对角线,并将小矩形的对角线折到原矩形的长边上.设MN的长为2,在下面给出的三种折叠中能得到长为($\sqrt{5}$-1)线段的有( )
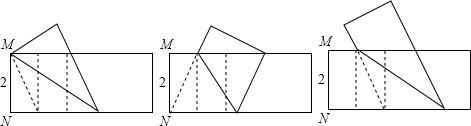

| A. | 0种 | B. | 1种 | C. | 2种 | D. | 3种 |
12.一场足球比赛采用单循环淘汰赛,每队进行5场比赛,每场比赛中胜得3分,和得2分,负得0分,得分最少的会被淘汰,如果其中两队的得分一样,则要计算得失球差来决定胜负.结果北方队和风暴队的成绩最好,同样是3胜、1和、1负,他们各场比赛记录如下:
由以上提供的信息回答下面问题.
(1)两队的得分各是多少?得失球差是多少?
(2)哪个队会被淘汰?
| 队伍/场次 | 1 | 2 | 3 | 4 | 5 |
| 北方队 | 和2:2 | 胜3:1 | 负0:1 | 胜2:1 | 胜3:2 |
| 风暴队 | 胜3:2 | 负0:2 | 胜2:1 | 和2:2 | 和2:2 |
(1)两队的得分各是多少?得失球差是多少?
(2)哪个队会被淘汰?
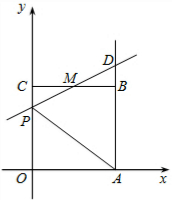 矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根
矩形OABC两邻边长a、b是关于x的方程x2-(k+1)x+$\frac{1}{4}$k2+$\frac{7}{4}$=0的两根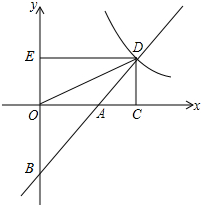 如图,直线y=x+b(b<0)与两坐标轴分别交于A,B两点,与双曲线y=$\frac{2}{x}(x>0)$交于点D,过点D作两坐标轴的垂线DC,DE,连结OD.
如图,直线y=x+b(b<0)与两坐标轴分别交于A,B两点,与双曲线y=$\frac{2}{x}(x>0)$交于点D,过点D作两坐标轴的垂线DC,DE,连结OD.