题目内容
15.Rt△ABC中,BC为较长的直角边,它是较短直角边长的两倍,把△ABC放入直角坐标系,若点B,点C的坐标分别为(1,2),(3,4),则点A的坐标为A1(2,5),A2(4,3),A3(0,3),A4(2,1).分析 由点B,点C的坐标分别为(1,2),(3,4),利用两点间的距离公式求出BC=$\sqrt{(3-1)^{2}+(4-2)^{2}}$=2$\sqrt{2}$.设点A的坐标为(x,y),分两种情况进行讨论:①如果∠ACB=90°,那么AC=$\sqrt{2}$,AB=$\sqrt{10}$,依此列出方程组$\left\{\begin{array}{l}{(x-3)^{2}+(y-4)^{2}=2}\\{(x-1)^{2}+(y-2)^{2}=10}\end{array}\right.$;②如果∠ABC=90°,那么AB=$\sqrt{2}$,AC=$\sqrt{10}$,依此列出方程组$\left\{\begin{array}{l}{(x-1)^{2}+(y-2)^{2}=2}\\{(x-3)^{2}+(y-4)^{2}=10}\end{array}\right.$,解方程组即可求出点A的坐标.
解答 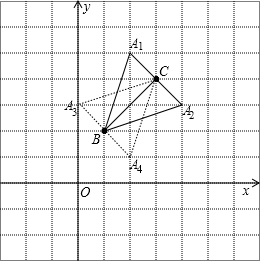 解:∵点B,点C的坐标分别为(1,2),(3,4),
解:∵点B,点C的坐标分别为(1,2),(3,4),
∴BC=$\sqrt{(3-1)^{2}+(4-2)^{2}}$=2$\sqrt{2}$.
∵Rt△ABC中,BC为较长的直角边,它是较短直角边长的两倍,
∴较短直角边长是$\sqrt{2}$,斜边长是$\sqrt{8+2}$=$\sqrt{10}$.
设点A的坐标为(x,y),BC为直角边时,分两种情况:
①如果∠ACB=90°,那么AC=$\sqrt{2}$,AB=$\sqrt{10}$,
则$\left\{\begin{array}{l}{(x-3)^{2}+(y-4)^{2}=2}\\{(x-1)^{2}+(y-2)^{2}=10}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,或$\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$,
∴A1(2,5),A2(4,3);
②如果∠ABC=90°,那么AB=$\sqrt{2}$,AC=$\sqrt{10}$,
则$\left\{\begin{array}{l}{(x-1)^{2}+(y-2)^{2}=2}\\{(x-3)^{2}+(y-4)^{2}=10}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$,或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴A3(0,3),A4(2,1);
即点A的坐标为A1(2,5),A2(4,3),A3(0,3),A4(2,1).
故答案为A1(2,5),A2(4,3),A3(0,3),A4(2,1).
点评 本题考查了勾股定理,两点间的距离公式,二元二次方程组的解法,坐标与图形性质,分类讨论是解题的关键.

 53天天练系列答案
53天天练系列答案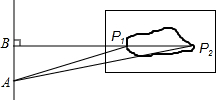 如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )
如图是一跳远运动员跳远时落在沙坑的痕迹,则表示该运动员成绩的是( )| A. | 线段AP1的长度 | B. | 线段AP2的长度 | C. | 线段BP2的长度 | D. | 线段BP1的长度 |
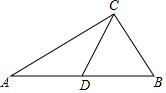 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )| A. | $\frac{\sqrt{17}-1}{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | $\frac{4}{3}$$\sqrt{3}$ |
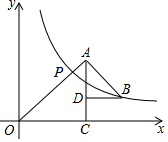 如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )
如图所示,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=$\frac{k}{x}$在第一象限的图象经过点B,与OA交于点P,且OA2-AB2=18,则点P的横坐标为( )| A. | 9 | B. | 6 | C. | 3 | D. | 3$\sqrt{2}$ |
| A. | 对石家庄市辖区内地下水水质情况的调查 | |
| B. | 对一个社区每天丢弃塑料袋数量的调查 | |
| C. | 对乘坐飞机的旅客是否携带违禁物品的调查 | |
| D. | 对河北电视台“中华好诗词”栏目收视率的调查 |
 如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )
如图,四边形ACDB内接于⊙O,若∠BDC=∠BOC,则∠BAC的度数为( )| A. | 50° | B. | 60° | C. | 45° | D. | 90° |

