题目内容
13.已知△ABC的三边分别为7,24,25.(1)求这个三角形外心与重心之间的距离;
(2)以这个三角形的最大角的顶点为圆心作一圆与最长边相切,求这个圆的直径之长.
分析 (1)由三角形的三边可得,△ABC是直角三角形,设O是斜边AB中点,可得O是△ABC的外心,由重心的性质可知:AE:EO=2:1,即可求出OE的值,
(2)先作CF⊥AB于点F,可得CF就是所求圆的半径,利用射影定理可得CF•AB=AC•CB,可得出CF的值,即可得出这个圆的直径之长.
解答 解:如图1,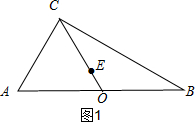
∵72+242=252,
∴△ABC是直角三角形,
设O是斜边AB中点,
∴O是△ABC的外心,
由重心的性质可知,AE:EO=2:1,
∴OE=$\frac{1}{3}$CO=$\frac{1}{3}$×$\frac{25}{2}$=$\frac{25}{6}$,
(2)如图2,作CF⊥AB于点F,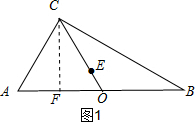
∴CF就是所求圆的半径,
∵CF•AB=AC•CB,
∴CF×25=7×24,解得CF=$\frac{168}{25}$,
∴直径为:$\frac{168}{25}$×2=$\frac{336}{25}$.
点评 本题主要考查了三角形的外心与内心,解题的关键是正确的找出外心与重心.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
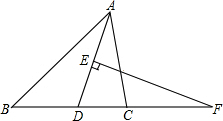 如图,在△ABC中,FD2=FB•FC,AD的垂直平分线交AD于E,交BC的延长线于F,求证:AD平分∠BAC.
如图,在△ABC中,FD2=FB•FC,AD的垂直平分线交AD于E,交BC的延长线于F,求证:AD平分∠BAC.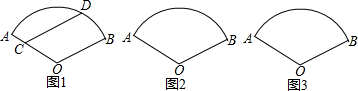
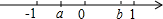 表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.
表示实数a,b的点在数轴上的位置如图所示,化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+|b-a|.