题目内容
18. 如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )| A. | 40° | B. | 30° | C. | 70° | D. | 60° |
分析 根据等腰三角形两底角相等求出∠B,再根据翻折的性质可得∠CED=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答 解:∵AB=AC,∠A=40°,
∴∠B=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-40°)=70°,
∵△ABC沿CD折叠,点B落在边AC上的点E处,
∴∠CED=∠B=70°,
由三角形的外角性质得,∠ADE=∠CED-∠A=70°-40°=30°.
故选B.
点评 本题考查了翻折变换的性质,等腰三角形的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,要注意折叠前后对应角相等.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
9.计算:2x2•(-3x3)的结果是( )
| A. | -6x5 | B. | 6x5 | C. | 5x5 | D. | -5x5 |
6.下列四个图形中,经过折叠可以围成一个棱柱的是( )
| A. |  | B. |  | C. |  | D. |  |
13.如果三角形的两边长分别为3和5,那么这个三角形的周长可能是( )
| A. | 9 | B. | 10 | C. | 15 | D. | 16 |
3. 如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
 如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
如图,在△ABC中,∠C=90°,BC=3,D,E分别在AB,AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )| A. | $\frac{1}{2}$ | B. | 3 | C. | 2 | D. | 1 |
10. 如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )
如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )
 如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )
如图,线段(每一线段长为1厘米)比例尺化成数值比例尺是( )| A. | 1:40 | B. | 1:80 | C. | 1:4000 | D. | 1:8000 |
7.从1,2,3这三个数字中随机抽取两个,抽取的这两个数的和是奇数的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
8.如果规定向东行进为正,那么-50m表示的意义是( )
| A. | 向东行进50m | B. | 向南行进50m | C. | 向西行进50m | D. | 向北行进50m |
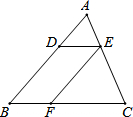 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.