题目内容
8.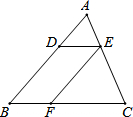 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于5:8.
分析 根据平行线分线段成比例定理,由DE∥BC得到AE:EC=AD:DB=3:5,则利用比例性质得到CE:CA=5:8,然后利用EF∥AB可得到CF:CB=5:8.
解答 解:∵DE∥BC,
∴AE:EC=AD:DB=3:5,
∴CE:CA=5:8,
∵EF∥AB,
∴CF:CB=CE:CA=5:8.
故答案为5:8.
点评 本题考查了平行线分线段成比例:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.

练习册系列答案
相关题目
18.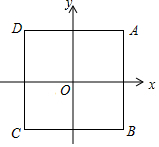 如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为( )
如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为( )
 如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为( )
如图,以正方形ABCD的中心为原点建立平面直角坐标系,点A的坐标为(2,2),则点D的坐标为( )| A. | (2,2) | B. | (-2,2) | C. | (-2,-2) | D. | (2,-2) |
19.在平面直角坐标系中,函数y=x2-2x的图象为C1,C1关于原点对称的图象为C2,则直线y=a(a为常数)与C1、C2的交点共有( )
| A. | 2个 | B. | 1个或2个或3个 | ||
| C. | 2个或3个或4个 | D. | 1个或2个或3个或4个 |
3.已知三角形的两边长为5,9,则第三边的长度可能是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13. 已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
 已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )
已知,如图,OC是∠AOB内部的一条射线,P是射线OC上任意点,PD⊥OA,PE⊥OB,下列条件中:①∠AOC=∠BOC,②PD=PE,③OD=OE,④∠DPO=∠EPO,能判定OC是∠AOB的角平分线的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20. 如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
 如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )
如图,在△ABC中,CD是∠ACB的平分线,∠B=40°,∠A=80°,那么∠BDC=( )| A. | 80° | B. | 90° | C. | 100° | D. | 110° |
17. 如图,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
如图,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
 如图,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )
如图,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是( )| A. | 20° | B. | 25° | C. | 35° | D. | 40° |
18. 如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )
 如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,将△ABC沿CD折叠,使点B落在边AC上的点E处,则∠ADE的度数是( )| A. | 40° | B. | 30° | C. | 70° | D. | 60° |