题目内容
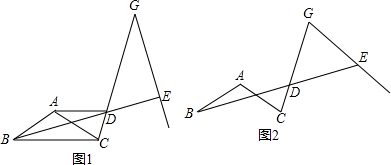
15.如图1,在等腰△ABC中,AB=AC,∠ABC=α,过点A作BC的平行线与∠ABC的平分线交于点D,连接CD.(1)求证:AC=AD;
(2)点G为线段CD延长线上一点,将GC绕着点G逆时针旋转β,与射线BD交于点E.
①如图1,若β=α,DG=2AD,试判断BC与EG之间的数量关系,并证明你的结论;
②若β=2α,DG=kAD,请直接写出$\frac{{S}_{△DEG}}{{S}_{△BCD}}$的值(用含k的代数式表示).
分析 (1)利用平行线的性质得出∠1=∠3,进而利用等腰三角形的性质得出AC=AD即可;
(2)利用已知得出∠GDE=∠BDC=90°-α,进而得出∠DEG=∠AHB=90°,则△DEG∽△AHB,进而利用相似三角形的性质得出答案;
(3)利用(2)得出∠AHB=∠DFG=90°,进而利用角平分线的性质以及相似三角形的判定与性质得出即可.
解答 解:如图1 (1)证明:∵BD平分∠ABC,
(1)证明:∵BD平分∠ABC,
∴∠1=∠2.
∵AD∥BC,
∴∠2=∠3.
∴∠1=∠3.
∴AB=AD.
∵AB=AC,
∴AC=AD.
(2)如图2证明:过A作AH⊥BC于点H.
由题意可得:∠AHB=90°.
∵AB=AC,∠ABC=α,
∴∠ACB=∠ABC=α.
∴∠BAC=180°-2α.
由(1)得AB=AC=AD.
∴点B、C、D在以A为圆心,AB为半径的圆上.
∴∠BDC=$\frac{1}{2}$∠BAC.
∴∠GDE=∠BDC=90°-α,
∵∠G=β=α=∠ABC,
∴∠G+∠GDE=90°.
∴∠DEG=∠AHB=90°.
∴△DEG∽△AHB.
∵GD=2AD,AB=AD,
∴DG=2AB,
∴$\frac{DG}{AB}$=$\frac{GE}{BH}$=2,
∵BC=2BH,
∴BC=GE;
(3)如图3,$\frac{{S}_{△DEG}}{{S}_{△BCD}}{=k}^{2}$. 理由:解:过A作AH⊥BC于点H,作∠DGE的平 分线GF,
理由:解:过A作AH⊥BC于点H,作∠DGE的平 分线GF,
∵由①得,∠DGF+∠GDE=90°,
∵∠AHB=∠DFG=90°.
又∵∠ABC=∠DGF=α,
∴△DFG∽△AHB.
又∵AB=AD,
$\frac{{S}_{△DFG}}{{S}_{△AHB}}=\frac{{GD}^{2}}{{AB}^{2}}=\frac{{GD}^{2}}{{AD}^{2}}{=k}^{2}$,
∵$\frac{{S}_{△DEG}}{{S}_{ABC}}=\frac{{2S}_{△DFG}}{{2S}_{△AHB}}{=k}^{2}$,
又∵S△ABC=S△BCD,
∴$\frac{{S}_{△DEG}}{{S}_{△BCD}}{=k}^{2}$.
点评 此题主要考查了相似三角形的判定与性质以及平行线的性质等知识,得出△ABH∽△DGF是解题关键.

 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
| A. | 辽宁省人数 | B. | 丹东市人数 | C. | 某中学学生数 | D. | 我班人数 |
| A. |  | B. |  | C. |  | D. |  |
 如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,求旗杆的高度?
如图,AC是操场上直立的一个旗杆,从旗杆上的B点到地面C涂着红色的油漆,用测角仪测得地面上的D点到B点的仰角是∠BDC=45°,到A点的仰角是∠ADC=60°(测角仪的高度忽略不计)如果BC=3米,求旗杆的高度?