题目内容
4.若x+y+z=3,求$\frac{(x-1)(y-1)(z-1)}{(x-1)^{3}+(y-1)^{3}+(z-1)^{3}}$的值.分析 根据x+y+z=3可设x-1=a,y-1=b,z-1=c,则a+b+c=(x+y+z)-3=0,c=-(a+b),再把a,b,c的值代入原式进行计算即可.
解答 解:∵设x-1=a,y-1=b,z-1=c,则a+b+c=(x+y+z)-3=0,
∴c=-(a+b),
∴原式=$\frac{abc}{{a}^{3}+{b}^{3}+{c}^{3}}$=$\frac{-ab(a+b)}{{a}^{3}+{b}^{3}-(a+b)^{3}}$=$\frac{-ab(a+b)}{-3ab(a+b)}$=$\frac{1}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
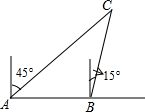 如图所示,在一条笔直的公路旁有A,B两个公交站台相距800米,居民区C位于A站台的北偏东45°方向,位于B站台的北偏东15°方向.
如图所示,在一条笔直的公路旁有A,B两个公交站台相距800米,居民区C位于A站台的北偏东45°方向,位于B站台的北偏东15°方向. 如图,△ABC中,P为BC边上的一点,PD∥AC,PE∥AB,说明∠DPE=∠BAC的理由.
如图,△ABC中,P为BC边上的一点,PD∥AC,PE∥AB,说明∠DPE=∠BAC的理由.