题目内容
10.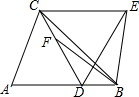 在△ABC中,∠A=60°,∠ABC=45°,点D是边AB上任意一点,连接CD.若∠BCD=15°,以线段CD为边在CD的有上方作正△CDE,连接BE,点F在线段CD上,且CF=BD,连接BF.求证:BE=BF.
在△ABC中,∠A=60°,∠ABC=45°,点D是边AB上任意一点,连接CD.若∠BCD=15°,以线段CD为边在CD的有上方作正△CDE,连接BE,点F在线段CD上,且CF=BD,连接BF.求证:BE=BF.
分析 连接EF,根据已知条件得到∠CDA=60°,由∠A=60°,推出△ACD为等边三角形,证得∠CDA=60°,由于△CDE是等边三角形,CE=DE,得到∠ECD=∠CDE=60°,根据全等三角形的性质得到∠1=∠2,EF=EB,推出△EFB是等边三角形,于是得到BE=BF.
解答 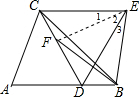 证明:连接EF,
证明:连接EF,
∵∠ABC=45°,∠BCD=15°,
∴∠CDA=60°,
∵∠A=60°,
∴△ACD为等边三角形,
∴∠CDA=60°,
∵△CDE是等边三角形,CE=DE,
∴∠ECD=∠CDE=60°,
∴∠EDB=180°-∠CDA-∠CDE=60°,
在△ECF与△EDB中,
$\left\{\begin{array}{l}{CE=DE}\\{∠ECF=∠EDB=60°}\\{CF=BD}\end{array}\right.$,
∴△ECF≌△EDB,
∴∠1=∠2,EF=EB,
∵△CDE是等边三角形,
∴∠1+∠3=60°,
∴∠2+∠3=60°,
∵EF=EB,
∴△EFB是等边三角形,
∴BE=BF.
点评 本题考查了全等三角形的判定和性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各式正确的是( )
| A. | $±\sqrt{0.36}$=±0.6 | B. | $\sqrt{9}=±3$ | C. | $\root{3}{(-3)^{3}}$=3 | D. | $\sqrt{(-2)^{2}}$=-2 |
18.已知命题:若a>b,则$\frac{1}{a}<\frac{1}{b}$.下列哪个反例可以说明这是个假命题( )
| A. | a=2,b=1 | B. | a=2,b=-1 | C. | a=1,b=2 | D. | a=-2,b=-1 |
5.函数y=$\frac{\sqrt{4-x}}{x-2}$中,自变量x的取值范围是( )
| A. | x<4 | B. | x≤4 | C. | x≤4且x≠2 | D. | x>2 |
15.下列运算正确的是( )
| A. | a-2=-$\frac{1}{{a}^{2}}$(a≠0) | B. | $\sqrt{(-2)^{2}}$=-2 | C. | a0=0(a≠0) | D. | $\root{3}{(-2)^{3}}$=-2 |
19.x取( )时,式子$\frac{\sqrt{x-2}}{x-1}$在实数范围内有意义.
| A. | x≥1且x≠2 | B. | x≥2且x≠1 | C. | x≥2 | D. | 都不正确 |
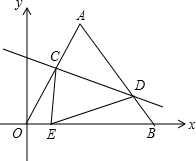 如图坐标系中,O(0,0),A(6,6$\sqrt{3}$),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE=$\frac{24}{5}$,则CE:DE的值是$\frac{7}{8}$.
如图坐标系中,O(0,0),A(6,6$\sqrt{3}$),B(12,0),将△OAB沿直线线CD折叠,使点A恰好落在线段OB上的点E处,若OE=$\frac{24}{5}$,则CE:DE的值是$\frac{7}{8}$. 如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.
如图,直线l1与直线l2互相垂直,A,B是两个定点.C,D分别是直线l1,l2上的动点.试确定C,D两点的位置,使四边形ACDB的周长最短.