题目内容
5.函数y=$\frac{\sqrt{4-x}}{x-2}$中,自变量x的取值范围是( )| A. | x<4 | B. | x≤4 | C. | x≤4且x≠2 | D. | x>2 |
分析 根据被开方数是非负数、分母不能为零,可得答案.
解答 解:由y=$\frac{\sqrt{4-x}}{x-2}$,得4-x≥0且x-2≠0.
解得x≤4且x≠2.
故选:C.
点评 本题考查了函数自变量的取值范围,利用被开方数是非负数、分母不能为零得出4-x≥0且x-2≠0是解题关键.

练习册系列答案
相关题目
17.下列运算正确的是( )
| A. | 20=0 | B. | $\sqrt{4}$=±2 | C. | 2-1=$\frac{1}{2}$ | D. | 23=6 |
14.比较2,$\sqrt{5}$,$\root{3}{7}$的大小,正确的是( )
| A. | 2<$\sqrt{5}$<$\root{3}{7}$ | B. | 2<$\root{3}{7}$<$\sqrt{5}$ | C. | $\sqrt{5}$<$\root{3}{7}$<2 | D. | $\root{3}{7}$<2<$\sqrt{5}$ |
15.下列运算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | (a+b)2=a2+b2 | C. | (-a)3=-6a3 | D. | -(x-2)=2-x |
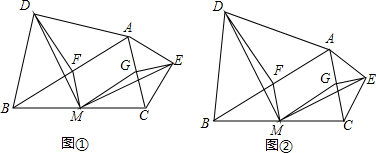
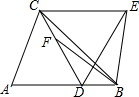 在△ABC中,∠A=60°,∠ABC=45°,点D是边AB上任意一点,连接CD.若∠BCD=15°,以线段CD为边在CD的有上方作正△CDE,连接BE,点F在线段CD上,且CF=BD,连接BF.求证:BE=BF.
在△ABC中,∠A=60°,∠ABC=45°,点D是边AB上任意一点,连接CD.若∠BCD=15°,以线段CD为边在CD的有上方作正△CDE,连接BE,点F在线段CD上,且CF=BD,连接BF.求证:BE=BF.