题目内容
6. 如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )
如图,一次函数y=-$\frac{2}{3}$x-4与正比例函数y=kx的图象交于第三象限内的点A,与y轴交于点B,且AO=AB,则正比例函数的解析式为( )| A. | y=$\frac{3}{4}$x | B. | y=$\frac{2}{3}$x | C. | y=$\frac{4}{3}$x | D. | y=$\frac{5}{6}$x |
分析 如图,过点A作AD⊥y轴于点D.根据一次函数解析式求得点B、C的坐标,结合等腰三角形的性质可以求得点D的坐标;通过锐角三角函数的定义求得点A的坐标;最后把点A的坐标代入正比例函数解析式y=kx即可求得k的值.
解答 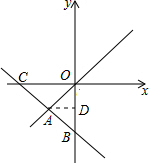 解:设正比例函数解析式y=kx.
解:设正比例函数解析式y=kx.
∵y=-$\frac{2}{3}$x-4,
∴B(0,-4),C(-6,0).
∴OC=6,OB=4.
如图,过点A作AD⊥y轴于点D.
又∵AO=AB,
∴OD=BD=2.
∴tan∠CBO=$\frac{OC}{OB}$=$\frac{AD}{BD}$,即$\frac{6}{4}$=$\frac{AD}{2}$,
解得AD=3.
∴A(-3,-2).
把点A的坐标代入y=kx,得
-2=-3k,
解得k=$\frac{2}{3}$.
故该函数解析式为:y=$\frac{2}{3}$x.
故选:B.
点评 本题考查了待定系数法求一次函数解析式.注意:①求点的坐标的方法是先求出这点到两坐标轴的距离,然后根据这点在坐标系中的位置写出这点的坐标.
②以后学了等腰三角形的性质后,作垂线后可直接得到OD=BD.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
17. 如图,在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,连接OA、OB,若OA⊥OB,OB=$\frac{\sqrt{2}}{2}$OA,则k的值为( )
如图,在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,连接OA、OB,若OA⊥OB,OB=$\frac{\sqrt{2}}{2}$OA,则k的值为( )
 如图,在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,连接OA、OB,若OA⊥OB,OB=$\frac{\sqrt{2}}{2}$OA,则k的值为( )
如图,在平面直角坐标系xOy中,已知第一象限内的点A在反比例函数y=$\frac{2}{x}$的图象上,第二象限内的点B在反比例函数y=$\frac{k}{x}$的图象上,连接OA、OB,若OA⊥OB,OB=$\frac{\sqrt{2}}{2}$OA,则k的值为( )| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | -$\frac{3}{2}$ |
14.下列四个图形:①等边三角形;②等腰梯形;③平行四边形;④正五边形,其中中心对称图形有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
16.如果用P表示某事件发生可能性的大小,已知一个随机事件发生的可能性很大,那么这个随机事件的P值可能是( )
| A. | 0.05 | B. | 0.95 | C. | 1 | D. | 15 |
 如图,将长方形ABCD沿对角线BD折叠,点C落在点C′处,若AB=2,则C′D的长是2.
如图,将长方形ABCD沿对角线BD折叠,点C落在点C′处,若AB=2,则C′D的长是2.



 小丽上午9:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中,小丽离家的距离y(米)和所经过的时间x(分)之间的函数关系图象如图所示.请根据图象回答下列问题:
小丽上午9:00从家里出发,骑车去一家超市购物,然后从这家超市返回家中,小丽离家的距离y(米)和所经过的时间x(分)之间的函数关系图象如图所示.请根据图象回答下列问题: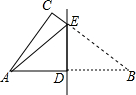 如图,在△ABC中,∠ACB=90°,DE⊥AB于点D,交BC边于点E,将△ABC沿直线DE折叠,点B恰好落在点A处,若AB=5,AC=3,则△ACE的周长为7.
如图,在△ABC中,∠ACB=90°,DE⊥AB于点D,交BC边于点E,将△ABC沿直线DE折叠,点B恰好落在点A处,若AB=5,AC=3,则△ACE的周长为7.