题目内容
如图所示,在RT△AO中, 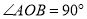 ,
, 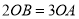 ,点
,点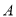 在反比例函数
在反比例函数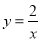 的图像上,若点
的图像上,若点 在反比例函数
在反比例函数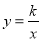 的图像上,则
的图像上,则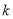 的值为( ).
的值为( ).
A. 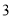 B.
B. 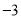 C.
C. 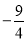 D.
D. 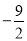
【答案】D
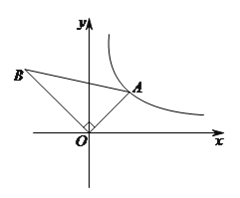
【解析】过点A,B作AC⊥x轴,BD⊥x轴,分别于C,D.
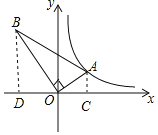
设点A的坐标是(m,n),则AC=n,OC=m,
∵∠AOB=90°,∴∠AOC+∠BOD=90°,
∵∠DBO+∠BOD=90°,∴∠DBO=∠AOC,
∵∠BDO=∠ACO=90°,∴△BDO∽△OCA,∴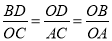 ,
,
∵2OB=3OA,∴BD=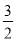 m,OD=
m,OD=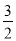 n,
n,
因为点A在反比例函数y=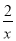 的图象上,则mn=2,
的图象上,则mn=2,
∵点B在反比例函数y=kx的图象上,B点的坐标是(?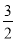 n ,
n , 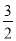 m),
m),
∴k=?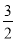 n?
n?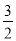 m=?
m=?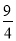 mn=?
mn=?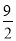 .
.
故选D.
【题型】单选题
【结束】
11
在函数y=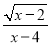 中,自变量x的取值范围是______.
中,自变量x的取值范围是______.
练习册系列答案
相关题目


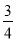 B.
B. 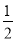 C.
C. 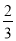 D.
D. 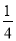

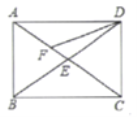
 AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形.
AC,由BE=DF证得OE=OF,根据对角线互相平分的四边形为平行四边形可判定四边形AECF是平行四边形,再证得AC=EF,根据对角线相等的平行四边形是矩形即可判定平行四边形AECF是矩形. AC,
AC, ,
, 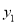 与
与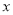 成正比例,
成正比例, 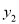 与
与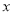 成反比例,并且当
成反比例,并且当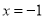 时,
时, 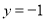 ,当
,当 时,
时, 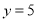 .
.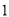 )求
)求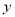 关于
关于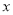 的函数关系式.
的函数关系式.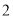 )当
)当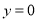 时,求
时,求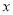 的值.
的值.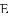
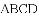
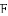
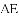
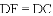


 .
. 的方程
的方程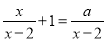 有增根,则
有增根,则 的值为__________.
的值为__________.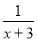 在实数范围内有意义,则实数
在实数范围内有意义,则实数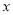 的取值范围是( ).
的取值范围是( ).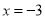 B.
B. 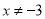 C.
C. 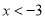 D.
D. 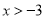
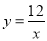 上的点是( ).
上的点是( ).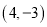 B.
B. 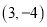 C.
C. 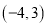 D.
D. 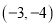
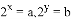 ,那么
,那么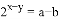 ;②满足条件
;②满足条件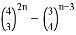 的n不存在;
的n不存在;