题目内容
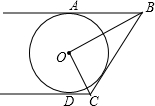 如图,已知AB、CD是⊙O的两条平行切线,A、D为切点,∠BOC=90°.求证:BC是⊙O的切线.
如图,已知AB、CD是⊙O的两条平行切线,A、D为切点,∠BOC=90°.求证:BC是⊙O的切线.考点:切线的判定与性质
专题:证明题
分析:如图,作辅助线,运用勾股定理首先证明xy=r2,然后运用三角形的面积公式证明OE=r,问题即可解决.
解答: 解:如图,连接AD,过点C作CF⊥AB于点F;
解:如图,连接AD,过点C作CF⊥AB于点F;
过点O作OE⊥BC于点E;
∵AB、CD是⊙O的两条平行切线,
∴AD为⊙O的直径,
∴OA⊥AB,OD⊥DC;四边形ADCF为矩形;
设⊙O的半径为r,AB=x,DC=y,BC=m;
则AF=DC=y,CF=AD=2r,BF=x-y;
由勾股定理得:
BC2=CF2+BF2,
即m2=(2r)2+(x-y)2①;
BC2=OB2+OC2,
即m2=x2+r2+y2+r2②,
由①、②知:
4r2+x2+y2-2xy=x2+y2+2r2,
∴xy=r2;
∵S△BOC=
BC•OE=
OB•OC,
∴
•OE=
•
,
∴OE=
=
,
∵xy=r2,
∴OE=
=r,
即圆心O到BC的距离等于⊙O的半径,
∴BC是⊙O的切线.
 解:如图,连接AD,过点C作CF⊥AB于点F;
解:如图,连接AD,过点C作CF⊥AB于点F;过点O作OE⊥BC于点E;
∵AB、CD是⊙O的两条平行切线,
∴AD为⊙O的直径,
∴OA⊥AB,OD⊥DC;四边形ADCF为矩形;
设⊙O的半径为r,AB=x,DC=y,BC=m;
则AF=DC=y,CF=AD=2r,BF=x-y;
由勾股定理得:
BC2=CF2+BF2,
即m2=(2r)2+(x-y)2①;
BC2=OB2+OC2,
即m2=x2+r2+y2+r2②,
由①、②知:
4r2+x2+y2-2xy=x2+y2+2r2,
∴xy=r2;
∵S△BOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴
| x2+y2+2r2 |
| x2+r2 |
| y2+r2 |
∴OE=
| ||||
|
=
|
∵xy=r2,
∴OE=
|
即圆心O到BC的距离等于⊙O的半径,
∴BC是⊙O的切线.
点评:该命题以圆为载体,以切线的判定为线索,以考查切线的性质、勾股定理的应用为核心构造而成;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
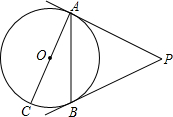 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径且AC=6,∠P=50°,求
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径且AC=6,∠P=50°,求
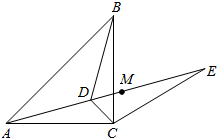 如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.
如图,已知点D为等腰直角△ABC内一点,∠BAD=∠ABD=30°,E为AD延长线上的一点,且CE=CA.



 如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为
如图,圆O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为