题目内容
?ABCD中，点P在对角线BD上（不与点B，D重合），添加一个条件，使得△BCD与△ADP相似，这个条件可以是 ．
考点：相似三角形的判定,平行四边形的性质
专题：开放型
分析：根据平行四边形对边平行性质可得一堆角相等，让另两对角中有一对相等即可证明△BCD与△ADP相似．
解答：解：∵AD∥BC，
∴∠ADP=∠CBD，
∵∠APD=∠C，
∴∠DAP=∠CDB，
∴△BCD∽△ADP．
故答案为∠APD=∠C．
∴∠ADP=∠CBD，
∵∠APD=∠C，
∴∠DAP=∠CDB，
∴△BCD∽△ADP．
故答案为∠APD=∠C．
点评：本题考查了相似三角形的判定，本题属于开放题，选出可以证明结论的一个条件是解题的关键．
练习册系列答案
相关题目
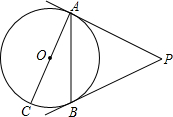如图，PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径且AC=6，∠P=50°，求
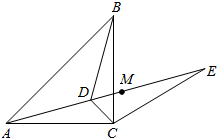如图，已知点D为等腰直角△ABC内一点，∠BAD=∠ABD=30°，E为AD延长线上的一点，且CE=CA．
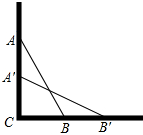一架云梯AB长25米，如图那样斜靠在一面墙AC上，这时云梯底端B离墙底C的距离BC为7米．