题目内容
13.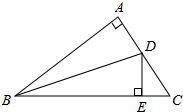 在△ABC中,已知∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,请解答下列问题:
在△ABC中,已知∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,请解答下列问题:(1)若AD=2cm,则D点到BC边的距离是2cm.
(2)若BC=7cm,则△CDE的周长为7cm.
(3)连接AE,试判断线段AE与BD的位置,并说明理由.
分析 (1)根据角平分线的性质定理解答;
(2)证明△ABD≌△EBD,得到BA=BE,根据三角形的周长公式计算即可;
(3)根据线段垂直平分线的判定定理解答.
解答 解:(1)∵BD平分∠ABC,DE⊥BC,∠A=90°,
∴DE=AD=2cm,
故答案为:2cm;
(2)在△ABD和△EBD中,
$\left\{\begin{array}{l}{∠ABD=∠EBD}\\{∠A=∠BED}\\{DA=DE}\end{array}\right.$,
∴△ABD≌△EBD,
∴BA=BE,
△CDE的周长=CD+CE+DE=CD+AD+CE=AC+CE=AB+CE=AE+CE=BC=7cm,
故答案为:7cm;
(3)∵DA=DE,BA=BE,
∴BD⊥AE.
点评 本题考查的是角平分线的性质定理,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知直线y=-x+m经过了(1,0)点,则关于x的不等式-x+m≥0的解集为( )
| A. | x<1 | B. | x>1 | C. | x≤1 | D. | 不确定 |
18.为了解2016年泰兴市八年级学生的视力情况,从中随机调查了500名学生的视力情况.下列说法正确的是( )
| A. | 2016年泰兴市八年级学生是总体 | |
| B. | 每一名八年级学生是个体 | |
| C. | 500名八年级学生是总体的一个样本 | |
| D. | 样本容量是500 |
5.下列各数中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{50}$ | B. | $\sqrt{24}$ | C. | $\sqrt{27}$ | D. | $\sqrt{\frac{1}{2}}$ |
3.若抛物线y=x2-2x+3不动,将平面直角坐标系xOy先沿水平方向向右平移一个单位,再沿铅直方向向上平移三个单位,则原抛物线图象的解析式应变为( )
| A. | y=(x-2)2+3 | B. | y=(x-2)2+5 | C. | y=x2-1 | D. | y=x2+4 |
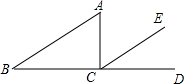 如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A﹦54°.
如图,点B、C、D在同一条直线上,CE∥AB,∠ACB=90°,如果∠ECD=36°,那么∠A﹦54°.