题目内容
5.下列各数中,与$\sqrt{3}$是同类二次根式的是( )| A. | $\sqrt{50}$ | B. | $\sqrt{24}$ | C. | $\sqrt{27}$ | D. | $\sqrt{\frac{1}{2}}$ |
分析 先把各项化简,再根据被开方数相同的即为同类二次根式.
解答 解:A、$\sqrt{50}$=5$\sqrt{2}$,与$\sqrt{3}$不是同类二次根式,故错误;
B、$\sqrt{24}$=2$\sqrt{6}$,与$\sqrt{3}$不是同类二次根式,故错误;
C、$\sqrt{27}=3\sqrt{3}$,与$\sqrt{3}$,是同类二次根式,故正确;
D、$\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$,与$\sqrt{3}$不是同类二次根式,故错误;
故选:C.
点评 本题考查了同类二次根式,解决本题的关键是熟记同类二次根式的定义.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
15.若0<a<1,下列比较a-1,a,a2的大小关系正确的是( )
| A. | a-1<a<a2 | B. | a<a-1<a2 | C. | a<a2<a-1 | D. | a2<a<a-1 |
16.?ABCD中,周长等于24,其中一组对边长是8,那么,另一组对边长为( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
15.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球试验,将球搅匀后,从中随机摸出一个球记下颜色,再把它放回袋中,不断重复,下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近于多少?
(2)假如你去摸一次,你摸到白球的可能性为多大?这时摸到黑球的可能性为多大?
(3)试估算口袋中黑、白两种颜色的球各有多少个?
(1)请估计:当n很大时,摸到白球的频率将会接近于多少?
| 摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的概率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(3)试估算口袋中黑、白两种颜色的球各有多少个?
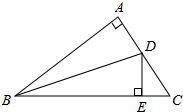 在△ABC中,已知∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,请解答下列问题:
在△ABC中,已知∠A=90°,AB=AC,BD平分∠ABC,DE⊥BC于E,请解答下列问题: