题目内容
 如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=
如图,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=| 1 |
| 3 |
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似?若存在,直接写出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)已知A、D、E三点的坐标,利用待定系数法可确定抛物线的解析式,进而能得到顶点B的坐标.
(2)过B作BM⊥y轴于M,由A、B、E三点坐标,可判断出△BME、△AOE都为等腰直角三角形,易证得∠BEA=90°,即△ABE是直角三角形,而AB是△ABE外接圆的直径,因此只需证明AB与CB垂直即可.BE、AE长易得,能求出tan∠BAE的值,结合tan∠CBE的值,可得到∠CBE=∠BAE,由此证得∠CBA=∠CBE+∠ABE=∠BAE+∠ABE=90°,此题得证.
(3)△ABE中,∠AEB=90°,tan∠BAE=
,即AE=3BE,若以D、E、P为顶点的三角形与△ABE相似,那么该三角形必须满足两个条件:①有一个角是直角、②两直角边满足1:3的比例关系;然后分情况进行求解即可.
(2)过B作BM⊥y轴于M,由A、B、E三点坐标,可判断出△BME、△AOE都为等腰直角三角形,易证得∠BEA=90°,即△ABE是直角三角形,而AB是△ABE外接圆的直径,因此只需证明AB与CB垂直即可.BE、AE长易得,能求出tan∠BAE的值,结合tan∠CBE的值,可得到∠CBE=∠BAE,由此证得∠CBA=∠CBE+∠ABE=∠BAE+∠ABE=90°,此题得证.
(3)△ABE中,∠AEB=90°,tan∠BAE=
| 1 |
| 3 |
解答:(1)解:由题意,设抛物线解析式为y=a(x-3)(x+1).
将E(0,3)代入上式,解得:a=-1.
∴y=-x2+2x+3.
则点B(1,4).
 (2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).
(2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).
在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE=
=3
在Rt△EMB中,EM=OM-OE=1=BM,
∴∠MEB=∠MBE=45°,BE=
=
∴∠BEA=180°-∠1-∠MEB=90°.
∴AB是△ABE外接圆的直径.
在Rt△ABE中,tan∠BAE=
=
=tan∠CBE,
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圆的切线.
(3)解:Rt△ABE中,∠AEB=90°,tan∠BAE=
,sin∠BAE=
,cos∠BAE=
;
若以D、E、P为顶点的三角形与△ABE相似,则△DEP必为直角三角形;
①DE为斜边时,P1在x轴上,此时P1与O重合;
由D(-1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO=
=tan∠BAE,即∠DEO=∠BAE
满足△DEO∽△BAE的条件,因此 O点是符合条件的P1点,坐标为(0,0).
②DE为短直角边时,P2在x轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE=
;
而DE=
=
,则DP2=DE÷sin∠DP2E=
÷
=10,OP2=DP2-OD=9
即:P2(9,0);
③DE为长直角边时,点P3在y轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE=
;
则EP3=DE÷cos∠DEP3=
÷
=
,OP3=EP3-OE=
;
综上,得:P1(0,0),P2(9,0),P3(0,-
).
将E(0,3)代入上式,解得:a=-1.
∴y=-x2+2x+3.
则点B(1,4).
 (2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).
(2)证明:如图1,过点B作BM⊥y于点M,则M(0,4).在Rt△AOE中,OA=OE=3,
∴∠1=∠2=45°,AE=
| OA2+OE2 |
| 2 |
在Rt△EMB中,EM=OM-OE=1=BM,
∴∠MEB=∠MBE=45°,BE=
| EM2+BM2 |
| 2 |
∴∠BEA=180°-∠1-∠MEB=90°.
∴AB是△ABE外接圆的直径.
在Rt△ABE中,tan∠BAE=
| BE |
| AE |
| 1 |
| 3 |
∴∠BAE=∠CBE.
在Rt△ABE中,∠BAE+∠3=90°,∴∠CBE+∠3=90°.
∴∠CBA=90°,即CB⊥AB.
∴CB是△ABE外接圆的切线.
(3)解:Rt△ABE中,∠AEB=90°,tan∠BAE=
| 1 |
| 3 |
| ||
| 10 |
3
| ||
| 10 |
若以D、E、P为顶点的三角形与△ABE相似,则△DEP必为直角三角形;
①DE为斜边时,P1在x轴上,此时P1与O重合;
由D(-1,0)、E(0,3),得OD=1、OE=3,即tan∠DEO=
| 1 |
| 3 |
满足△DEO∽△BAE的条件,因此 O点是符合条件的P1点,坐标为(0,0).
②DE为短直角边时,P2在x轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠DEP2=∠AEB=90°,sin∠DP2E=sin∠BAE=
| ||
| 10 |
而DE=
| 12+32 |
| 10 |
| 10 |
| ||
| 10 |
即:P2(9,0);
③DE为长直角边时,点P3在y轴上;
若以D、E、P为顶点的三角形与△ABE相似,则∠EDP3=∠AEB=90°,cos∠DEP3=cos∠BAE=
3
| ||
| 10 |
则EP3=DE÷cos∠DEP3=
| 10 |
3
| ||
| 10 |
| 10 |
| 3 |
| 1 |
| 3 |
综上,得:P1(0,0),P2(9,0),P3(0,-
| 1 |
| 3 |
点评:该题考查了二次函数的综合题,涉及到二次函数解析式的确定、切线的判定、相似三角形的判定、图形面积的解法等重点知识,综合性强,难度系数较大.此题的难点在于第三小题,它需要分情况进行讨论,容易出现漏解的情况.在解答动点类的函数问题时,一定不要遗漏对应的自变量取值范围.

练习册系列答案
相关题目
 如图是某中学初中各年级学生人数比例统计图,已知八年级学生540人,那么该校七年级学生人数为( )
如图是某中学初中各年级学生人数比例统计图,已知八年级学生540人,那么该校七年级学生人数为( )| A、405 | B、216 |
| C、473 | D、324 |
若函数y=
的图象在其所在的每一象限内,函数值y随自变量x的增大而减小,则m的取值范围是( )
| m+3 |
| x |
| A、m<-3 | B、m<0 |
| C、m>-3 | D、m>0 |
 看图填空:
看图填空:
 如图,已知三角形ABC的三个顶点的坐标分别为A(0.2),B(-3,1),C(-2,0),若将三角形ABC向右平移3个单位,再向下平移4个单位得到三角形A1B1C1.
如图,已知三角形ABC的三个顶点的坐标分别为A(0.2),B(-3,1),C(-2,0),若将三角形ABC向右平移3个单位,再向下平移4个单位得到三角形A1B1C1.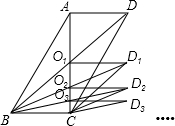 如图,?ABCD中,AC,BD交于点O1,作?BCD1O1,连接BD1交AC于点O2,作
如图,?ABCD中,AC,BD交于点O1,作?BCD1O1,连接BD1交AC于点O2,作