题目内容
3.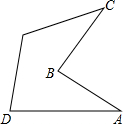 某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号).
某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号).
分析 直接构造直角三角形,再利用锐角三角函数关系得出BE,CF的长,进而得出答案.
解答  解:过点B作BE⊥AD于E,作BF∥AD,过C作CF⊥BF于F,
解:过点B作BE⊥AD于E,作BF∥AD,过C作CF⊥BF于F,
在Rt△ABE中,∵∠A=30°,AB=4m,
∴BE=2m,
由题意可得:BF∥AD,
则∠FBA=∠A=30°,
在Rt△CBF中,
∵∠ABC=75°,
∴∠CBF=45°,
∵BC=4m,
∴CF=sin45°•BC=2$\sqrt{2}$m,
∴C点到地面AD的距离为:(2$\sqrt{2}$+2)m.
点评 此题主要考查了解直角三角形的应用以及锐角三角函数关系,正确得出BE,CF的长是解题关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12.关于x的方程(a+3)x2-5x=0的解的情况是( )
| A. | 一个解 | B. | 两个解 | C. | 一个或两个解 | D. | 无解 |
 如图,点O在直线AB上,OC⊥OD,OC,OF分别平分∠AOE和∠BOD,若∠AOC=20°,则∠BOF的度数为35°.
如图,点O在直线AB上,OC⊥OD,OC,OF分别平分∠AOE和∠BOD,若∠AOC=20°,则∠BOF的度数为35°.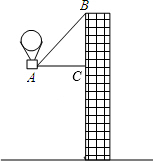 如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)
如图,有一热气球到达A处时,仪器显示其正前方一高楼顶部B的仰角是43°,与楼的水平距离AC为12米,为了安全飞越高楼,气球应至少再上升多少米?(结果精确到0.1米)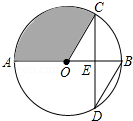 如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.
如图,AB是⊙O的直径,弦CD交AB于点E,且E为OB的中点,∠CDB=30°,CD=4$\sqrt{3}$,则阴影部分的面积$\frac{16}{3}$π.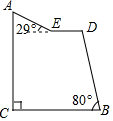 “蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)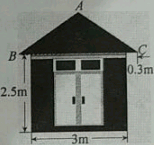 一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)
一个住宅区的配电房示意图如图所示,它是一个轴对称图形.已知∠ABC=35°,求配电房房顶离地面的高度(精确到0.1m).(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)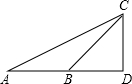 如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?
如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A,B两处的视角∠ACB是多少度?