题目内容
18.若正比例函数y=kx(k≠0)的图象过点(-3,9),则正比例函数y=(k+1)x的图象经过第二、四象限.分析 首先把(-3,9)代入正比例函数y=kx,计算出k的值,然后可确定y=(k+1)x的解析式,再根据正比例函数的性质可得答案.
解答 解:∵正比例函数y=kx(k≠0)的图象过点(-3,9),
∴9=-3k,
解得:k=-3,
∴正比例函数y=(k+1)x变为y=-2x,
∵-2<0,
∴图象经过第二、四象限.
故答案为:二、四.
点评 此题主要考查了正比例函数的性质,关键是掌握正比例函数图象的性质:它是经过原点的一条直线.当k>0时,图象经过一、三象限,y随x的增大而增大;当k<0时,图象经过二、四象限,y随x的增大而减小.

练习册系列答案
相关题目
6.如果正多边形的一个内角等于135°,那么这个正多边形的边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
7. 如图所示,图中共有相似三角形( )
如图所示,图中共有相似三角形( )
 如图所示,图中共有相似三角形( )
如图所示,图中共有相似三角形( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
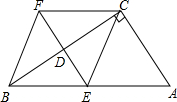 如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE,求证:四边形BEFC是菱形.
如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE,求证:四边形BEFC是菱形.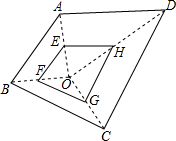 如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )
如图所示,E,F,G,H分别是OA,OB,OC,OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )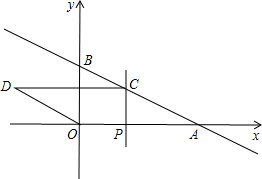 如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P为x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA、AC为边构造平行四边形OACD,设点P的横坐标为m.
如图,在平面直角坐标系中,直线y=kx+b经过点A(2,0),B(0,1),动点P为x轴正半轴上的动点,过点P作PC⊥x轴,交直线AB于点C,以OA、AC为边构造平行四边形OACD,设点P的横坐标为m.