题目内容
 已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.(1)求证:AD是⊙O的切线;
(2)如果PB是⊙O的切线,BC=4,求PE的长.
考点:切线的判定,相似三角形的判定与性质
专题:证明题
分析:(1)根据等腰三角形的性质由AB=AC,点D是边BC的中点得到AD⊥BC,然后根据切线的判定定理即可得到AD是⊙O的切线;
(2)连结OP,由于AD是⊙O的切线,PB是⊙O的切线,根据切线长定理得PE=DE,根据切线的性质得OP⊥PE,易证得△BDE∽△BPO,则
=
,由于BC=4,得到CD=BD=2,则OP=1,OB=3,利用勾股定理计算出BP=
=2
,然后利用相似比可计算出DE=
,所以PE=
.
(2)连结OP,由于AD是⊙O的切线,PB是⊙O的切线,根据切线长定理得PE=DE,根据切线的性质得OP⊥PE,易证得△BDE∽△BPO,则
| DE |
| OP |
| BD |
| BP |
| OB2-OP2 |
| 2 |
| ||
| 2 |
| ||
| 2 |
解答: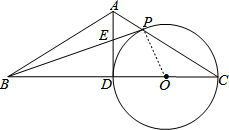 (1)证明:∵AB=AC,点D是边BC的中点,
(1)证明:∵AB=AC,点D是边BC的中点,
∴AD⊥BC,
∴AD是⊙O的切线;
(2)解:连结OP,如图,
∵AD是⊙O的切线,PB是⊙O的切线,
∴PE=DE,OP⊥PE,
∴∠BPO=90°,
∴∠BPO=∠ADB=90°,
而∠DBE=∠PBO,
∴△BDE∽△BPO,
∴
=
,
∵BC=4,
∴CD=BD=2,
∴OP=1,OB=3,
∴BP=
=
=2
,
∴DE=
=
,
∴PE=DE=
.
 (1)证明:∵AB=AC,点D是边BC的中点,
(1)证明:∵AB=AC,点D是边BC的中点,∴AD⊥BC,
∴AD是⊙O的切线;
(2)解:连结OP,如图,
∵AD是⊙O的切线,PB是⊙O的切线,
∴PE=DE,OP⊥PE,
∴∠BPO=90°,
∴∠BPO=∠ADB=90°,
而∠DBE=∠PBO,
∴△BDE∽△BPO,
∴
| DE |
| OP |
| BD |
| BP |
∵BC=4,
∴CD=BD=2,
∴OP=1,OB=3,
∴BP=
| OB2-OP2 |
| 32-12 |
| 2 |
∴DE=
| 1×2 | ||
2
|
| ||
| 2 |
∴PE=DE=
| ||
| 2 |
点评:本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.也考查了相似三角形的判定与性质和等腰三角形的性质.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
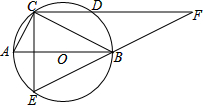 如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=
如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=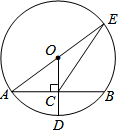 如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.
如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.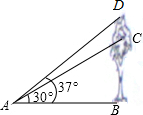 九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)
九年级1班的同学为了了解教学楼前一棵树生长情况,去年在教学楼前点A处测得树顶点C的仰角为30°,树高5米,今年他们仍在原地A处测得大树D的仰角为37°,问这棵树一年生长了多少米?(精确到0.01)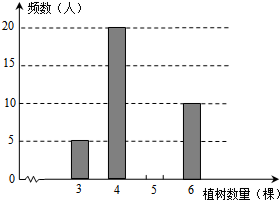 今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).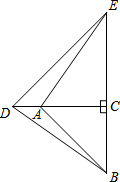 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.
如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD. 如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积.若关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为
如图,等腰梯形ABCD的底边AD在x轴上,顶点C在y轴正半轴上,B(4,2),一次函数y=kx-1的图象平分它的面积.若关于x的函数y=mx2-(3m+k)x+2m+k的图象与坐标轴只有两个交点,则m的值为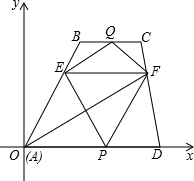 如图,在梯形ABCD中,BC∥AD,EF∥BC交AB于E,CD于F,P、Q分别为边AD和BC上的动点.若∠FAD=30°,AF=4
如图,在梯形ABCD中,BC∥AD,EF∥BC交AB于E,CD于F,P、Q分别为边AD和BC上的动点.若∠FAD=30°,AF=4