题目内容
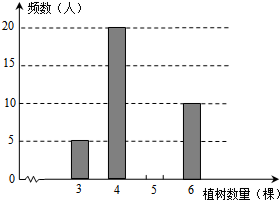 今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).
今年植树节,某校组织师生开展植树造林活动,为了了解全校1200名学生的植树情况,随机抽样调查部分学生的植树情况,制成如下统计表和条形统计图(均不完整).| 植树数量(棵) | 频数 | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | |
| 5 | 0.3 | |
| 6 | 10 | 0.2 |
| 合计 | 1 |
(2)求所抽样的学生植树数量的平均数;
(3)若植树数量不少于5棵的记为“表现优秀”,试根据抽样数据,估计该校1200名学生“表现优秀”的人数.
考点:条形统计图,频数与频率,频数(率)分布表
专题:
分析:(1)用总人数减去其他小组的人数即可求得植树棵树为5的小组的频数,除以总人数即可得到该组的频率;
(2)用加权平均数计算植树量的平均数即可;
(3)用样本的平均数估计总体的平均数即可.
(2)用加权平均数计算植树量的平均数即可;
(3)用样本的平均数估计总体的平均数即可.
解答:解:(1)填表如下:
补图如图所示:

(2)
=4.6(棵);
(3)由样本的数据知,“表现优秀”的百分率为0.3+0.2=0.5
由此可以估计该校1200名学生“表现优秀”的人数:1200×0.5=600(人);
| 植树数量(棵) | 频数 | 频率 |
| 3 | 5 | 0.1 |
| 4 | 20 | 0.4 |
| 5 | 15 | 0.3 |
| 6 | 10 | 0.2 |
| 合计 | 50 | 1 |

(2)
| 5×3+20×4+15×5+10×6 |
| 50 |
(3)由样本的数据知,“表现优秀”的百分率为0.3+0.2=0.5
由此可以估计该校1200名学生“表现优秀”的人数:1200×0.5=600(人);
点评:本题考查的是加权平均数的求法、频数分布直方图、用样本估计总体等知识.频率=频数÷总数,用样本估计整体让整体×样本的百分比即可.

练习册系列答案
相关题目
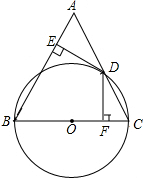 如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,
如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,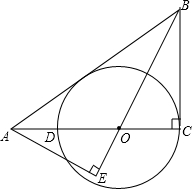 如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE.
如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE. 如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F. 已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.