题目内容
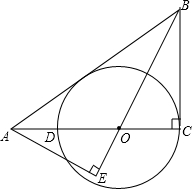
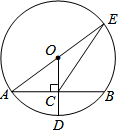 如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.
如图,⊙O的半径OD⊥弦AB于点C,联结AO并延长交⊙O于点E,联结EC.已知AB=8,CD=2.(1)求OA的长度;
(2)求CE的长度.
考点:垂径定理,勾股定理,圆周角定理
专题:
分析:(1)根据垂径定理得出AC=BC=
AB=4,根据勾股定理得出方程,求出即可;
(2)连接BE,求出OC∥BE且OC=
BE,求出BE,根据勾股定理求出CE即可.
| 1 |
| 2 |
(2)连接BE,求出OC∥BE且OC=
| 1 |
| 2 |
解答:(1)解:∵在⊙O中,OD⊥弦AB,
∴AC=BC=
AB,
∵AB=8,
∴AC=BC=4,
设OA为x,则OD=OA=x,
∵CD=2,
∴OC=x-2
在Rt△ACO中,AC2+OC2=AO2
∴42+(x-2)2=x2,
解得x=5,
∴OA=5;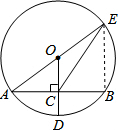
(2)解:连接BE,
∵OA=OE,AC=BC,
∴OC∥BE且OC=
BE,
∴∠EBA=∠OCA=90°,
∵OC=OD-CD=5-2=3,
∴BE=6,
在Rt△ECB中,BC2+EB2=EC2
∴42+62=EC2,
∴EC=2
.
∴AC=BC=
| 1 |
| 2 |
∵AB=8,
∴AC=BC=4,
设OA为x,则OD=OA=x,
∵CD=2,
∴OC=x-2
在Rt△ACO中,AC2+OC2=AO2
∴42+(x-2)2=x2,
解得x=5,
∴OA=5;

(2)解:连接BE,
∵OA=OE,AC=BC,
∴OC∥BE且OC=
| 1 |
| 2 |
∴∠EBA=∠OCA=90°,
∵OC=OD-CD=5-2=3,
∴BE=6,
在Rt△ECB中,BC2+EB2=EC2
∴42+62=EC2,
∴EC=2
| 13 |
点评:本题考查了勾股定理,垂径定理,圆周角定理,三角形中位线的应用,用了方程思想,题目比较典型,难度适中.

练习册系列答案
相关题目
将
-
=1变形为
x=1-
,其错在( )
| x |
| 0.5 |
| 1 |
| 0.7 |
| 10 |
| 5 |
| 10 |
| 7 |
| A、不应将分子、分母同时扩大10倍 |
| B、移项未改变符号 |
| C、1未乘以10 |
| D、以上都不是 |
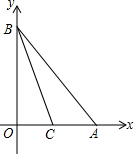 如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,已知S△BOC=S△ABC,
如图,点A和点B分别在x轴和y轴上,且OA=OB=4,直线BC交x轴于点C,已知S△BOC=S△ABC,
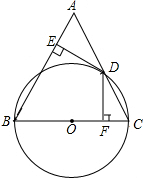 如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,
如图,在ABC中,AB=BC,以BC为直径的⊙O交AC于点D,过点D作DE⊥AB,DF⊥BC,垂足分别为E、F,
 如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE.
如图,△ABC中,∠C=90°,O点在AC边上,以O为圆心,OC为半径的圆与AC的另一个交点为D,AE⊥BO的延长线于E点,且AE2=OE•BE. 已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.
已知:如图,在△ABC中,AB=AC,点D是边BC的中点.以CD为直径作⊙O,交边AC于点P,连接BP,交AD于点E.