题目内容
10. 如图,已知O为△ABC的外心,P为弧$\widehat{AB}$上一点,过P分别作OA、OB的垂线,它们与△ABC各边的交点如图,若PM=MS,求证:PN=NT.
如图,已知O为△ABC的外心,P为弧$\widehat{AB}$上一点,过P分别作OA、OB的垂线,它们与△ABC各边的交点如图,若PM=MS,求证:PN=NT.
分析 如图,连接PB、PA,延长PT交⊙O于E,延长PS交⊙O于F,首先证明PN=PM,由△PBN∽△APM,△NTB∽△MAS,推出PM2=SM•NT,根据PM=PN=SM,即可证明.
解答 证明:如图,连接PB、PA,延长PT交⊙O于E,延长PS交⊙O于F.
∵OB⊥PE,OA⊥PF,
∴$\widehat{PB}$=$\widehat{PE}$,$\widehat{PA}$=$\widehat{AF}$,
∴∠1=∠2,∠3=∠4,
∵∠5=∠1+∠4,∠6=∠2+∠3,
∴∠5=∠6,△PBN∽△APM,
∴PN=PM,$\frac{PN}{AM}$=$\frac{BN}{AM}$,
∴PM2=BN•AM,
∵$\widehat{AB}$=$\widehat{PB}$+$\widehat{PA}$=$\widehat{BE}$+$\widehat{PA}$,
∴∠C=∠1+∠4,
∵∠4+∠CBA+∠1+∠4=180°,∠C+∠CBA+∠CAB=180°,
∴∠4=∠CAB,
∵∠5=∠BNT,∠6=∠AMS,
∴△NTB∽△MAS,
∴$\frac{BN}{SM}$=$\frac{NT}{AM}$,
∴SM•NT=BN•AM,
∴PM2=SM•NT,
∵PM=SM=PN,
∴PN2=PN•NT,
∴PN=NT.
点评 本题考查三角形外接圆-外心、相似三角形的判定和性质,垂径定理等知识,解题的关键是学会添加辅助线、构造相似三角形解决问题,题目比较难,用了两次相似,属于竞赛类题目.

练习册系列答案
相关题目
20.已知A(x1,2009)、B(x2,2009)是二次函数y=ax2+bx+8(a≠0)的图象上两点,则当x=x1+x2时,二次函数的值为( )
| A. | $\frac{2{b}^{2}}{a}$+8 | B. | 2009 | C. | 8 | D. | 无法确定 |
 如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上.
如图,某仓储中心有一斜坡AB,其坡度为i=1:2,顶部A处的高AC为4m,B、C在同一水平地面上. 如图,四边形ABCD中,BC∥AD,BC=AB,∠BAD=90°,∠D=45°,E是BC上一点,F是CD上一点,
如图,四边形ABCD中,BC∥AD,BC=AB,∠BAD=90°,∠D=45°,E是BC上一点,F是CD上一点,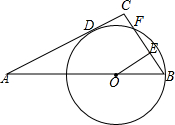 如图,Rt△ABC,∠C=90°,BC=3,点O在AB上,OB=2,以OB长为半径的⊙O与AC相切于点D,交BC于点F,OE⊥BC于点E,则弦BF的长为2.
如图,Rt△ABC,∠C=90°,BC=3,点O在AB上,OB=2,以OB长为半径的⊙O与AC相切于点D,交BC于点F,OE⊥BC于点E,则弦BF的长为2.