Question

2．如图，四边形ABCD中，BC∥AD，BC=AB，∠BAD=90°，∠D=45°，E是BC上一点，F是CD上一点，
（1）若EF⊥AE，求证：AE=EF．
（2）若AE=EF，求证：EF⊥AE．

Answer 1

分析 （1）在BA上截取BG=BE，先证明∠EGA=∠FCE，AG=CE，∠CEF=∠GAE，进而判定△AGE≌△ECF（ASA），最后得出结论AE=EF；
（2）在BA上截取BP=BE，作AM⊥EP于M，延长PE交FC的延长线于N．先证明△APM≌△CEN，推出AM=EN，再证明△AEM≌△EFN，推出∠AEM=∠EFN，由∠EFN+∠FEN=90°，推出∠AEM+∠FEN=90°，由此即可解得出结论．

解答 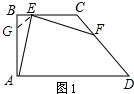证明：（1）如图1，取BG=BE，连结GE．
∵∠BAD=90°，BE=BG，
∴∠BGE=45°，
∴∠EGA=135°，
∵BC∥AD，
∴∠D+∠FCE=180°，
∴∠FCE=135°，
∴∠EGA=∠FCE=135°，
∵EF⊥AE，
∴∠AEF=90°，
∴∠CEF+∠AEB=90°，
又∵∠AEB+∠EAB=90°，
∴∠CEF=∠GAE，
∵BA=BC，BE=BG，
∴AG=EC，
在△AGE和△ECF中，
$\left\{\begin{array}{l}{∠EGA=∠FCE=135°}\\{AG=EC}\\{∠CEF=∠GAE}\end{array}\right.$，
∴△AGE≌△ECF（ASA），
∴AE=EF．
（2）如图，在BA上截取BP=BE，作AM⊥EP于M，延长PE交FC的延长线于N．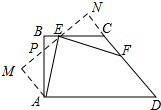
∵AB=BC，∠B=90°，
∴∠BPE=∠BEP=45°，AP=EC，
∵∠D=45°，BC∥AD，
∴∠ECN=45°，
∵∠PEB=∠CEN=45°，
∴∠N=90°=∠M，∠APM=∠BPE=45°，
在△APM和△ECN中，
$\left\{\begin{array}{l}{∠M=∠N=90°\\;}\\{∠APM=∠CEN}\\{AP=EC}\end{array}\right.$，
∴△APM≌△CEN（AAS），
∴AM=CN=EN，
在Rt△AEM和Rt△EFN中，
$\left\{\begin{array}{l}{AE=EF\\;}\\{AM=EN}\end{array}\right.$，
∴Rt△AEM≌Rt△EFN（HL），
∴∠AEM=∠EFN，
∵∠EFN+∠FEN=90°，
∴∠AEM+∠FEN=90°，
∴∠AEF=90°，
即EF⊥AE．

点评 本题主要考查了全等三角形的判定和性质、平行线的性质以及等腰直角三角形的性质等知识，在判定三角形全等时，关键是选择恰当的判定条件，必要时添加适当辅助线构造全等三角形．