题目内容
6.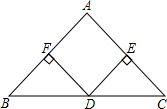 已知:如图,在△ABC中,AB=AC,D是的BC边的中点,DE⊥AC,DF⊥AB,垂足
已知:如图,在△ABC中,AB=AC,D是的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E、F.
(1)求证:DE=DF;
(2)只添加一个条件,使四边形EDFA是正方形,并给出证明.
分析 (1)连接AD,根据等腰三角形的性质可得AD是∠BAC的角平分线,再根据角平分线的性质可得DE=DF;
(2)添加∠BAC=90°,根据三角形是直角的四边形是矩形可得四边形AFDE是矩形,再由条件DF=DE可得四边形EDFA是正方形.
解答 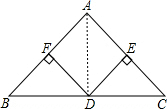 解:(1)连接AD,
解:(1)连接AD,
∵AB=AC,D是的BC边的中点,
∴AD是∠BAC的角平分线,
∵DE⊥AC,DF⊥AB,
∴DF=DE;
(2)添加∠BAC=90°,
∵DE⊥AC,DF⊥AB,
∴∠AFD=∠AED=90°,
∴四边形AFDE是矩形,
∵DF=DE,
∴四边形EDFA是正方形.
点评 此题主要考查了等腰三角形的性质,以及正方形的判定,关键是掌握等腰三角形三线合一的性质.

练习册系列答案
相关题目
15.某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件( )元.
| A. | 39 | B. | 40 | C. | 42 | D. | 45 |
 如图,A是反比例函数y=$\frac{k}{x}$的图象上一点,过点A作AB垂直于y轴于B,若△AOB的面积为3,则k的值是6.
如图,A是反比例函数y=$\frac{k}{x}$的图象上一点,过点A作AB垂直于y轴于B,若△AOB的面积为3,则k的值是6.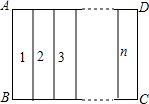 一块矩形绸布的宽AB=a m,长AD=1m,按照图中所示的方式将它裁成相同的n面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即,那么a的值应当是$\frac{\sqrt{n}}{n}$.
一块矩形绸布的宽AB=a m,长AD=1m,按照图中所示的方式将它裁成相同的n面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,即,那么a的值应当是$\frac{\sqrt{n}}{n}$.