题目内容
15.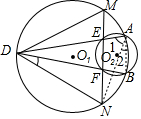 如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)
如图,已知⊙O1与⊙O2交于A,B,D为⊙O1上一点,DA,DB交⊙O2于E,F,EF交⊙O1于M,N,求证:DM=DN.(提示:连接AB、AN)
分析 连接AB,AN,根据圆内接四边形的性质得到∠BFN=∠BAE=∠1+∠2,由三角形的外角的性质得到∠BFN=∠3+∠DNM,∠2=∠3,等量代换得到∠DNM=∠1,根据圆周角定理得到∠1=∠M,求得∠M=∠DNM,于是得到结论.
解答  解:连接AB,AN,
解:连接AB,AN,
∵四边形ABFE是⊙O2的内接四边形,
∴∠BFN=∠BAE=∠1+∠2,
∵∠BFN=∠3+∠DNM,∠2=∠3,
∴∠DNM=∠1,
∵∠1=∠M,
∴∠M=∠DNM,
∴DM=DN.
点评 本题考查了两圆的位置关系,等腰三角形的判定,圆周角定理,圆内接四边形的性质,三角形的外角的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
4.下列约分正确的是( )
| A. | $\frac{{x}^{6}}{{x}^{2}}$=x3 | B. | $\frac{x+y}{{x}^{2}+xy}$=$\frac{1}{x}$ | C. | $\frac{x+y}{x+y}$=0 | D. | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ |
5.一次函数y=-2x+3的图象与x轴的交点坐标是( )
| A. | (0,3) | B. | (3,0) | C. | ($\frac{3}{2}$,0) | D. | ($\frac{2}{3}$,0) |
 如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论:
如图,正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展开后折痕DE分别交AB、AC于点E、G,连结GF,给出下列结论: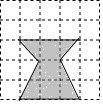 如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.
如图,方格图中小正方形的边长为1.将方格图中阴影部分图形剪下来,再把剪下的阴影部分重新剪拼成一个正方形(不重叠无缝隙),那么所拼成的这个正方形的边长为$\sqrt{6}$.