题目内容
11．
如图，已知△ACD∽△BCA，若CD=4，AC=6，则BC等于（ ）| A． | 9 | B． | 10 | C． | 11 | D． | 12 |
分析 由相似三角形的性质列出比例式，从而可求得BC的长．
解答 ∵△ACD∽△BCA，
∴$\frac{BC}{AC}=\frac{AC}{CD}$，即：$\frac{BC}{6}=\frac{6}{4}$．
解得：BC=9．
故选：A．
点评 本题主要考查的是相似三角形的性质的应用，根据相似三角形对应边成比例列出比例式是解题的关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知：AB∥CD，EF∥CD，且∠ABC=20°，∠CFE=30°，则∠BCF的度数是50°．
如图，∠1+∠2=145度．
19．已知梯形ABCD中，AD∥BC，则∠A：∠B：∠C：∠D不可能是（ ）
| A． | 3：7：5：5 | B． | 5：4：5：4 | C． | 4：5：6：3 | D． | 8：1：4：5 |
如图，直径为1的圆从原点沿数轴向右滚动一周，圆上原来与原点重合的点A到达点A′，则点A′表示的数是π．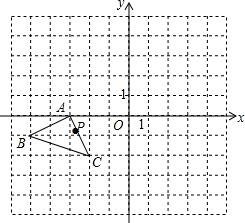
如图，在平面直角坐标系中，P（a，b）是△ABC的边AC上一点，△ABC经平移得到△A1B1C1，且点P的对应点为P1（a+5，b+4）．
20．下列各式正确的是（ ）
| A． | $\sqrt{9}$=±3 | B． | $\sqrt{（-7）^{2}}$=7 | C． | $\root{3}{9}$=3 | D． | （-$\sqrt{2}$）2=4 |
