题目内容
10. 如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.
如图,在矩形ABCD中,以B为圆心,BC长为半径作弧,交AD于E,连接BE,过C点作CF⊥BE于F.求证:BF=AE.
分析 利用矩形的性质得出AD∥BC,∠A=90°,再利用全等三角形的判定得出△BFC≌△EAB,进而得出答案.
解答 证明:在矩形ABCD中,AD∥BC,∠A=90°,
∴∠AEB=∠FBC,
∵CF⊥BE,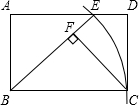
∴∠BFC=∠A=90°,
由作图可知,BC=BE,
在△BFC和△EAB中,
$\left\{\begin{array}{l}{∠A=∠CFB}\\{∠AEB=∠FBC}\\{EB=BC}\end{array}\right.$,
∴△BFC≌△EAB(AAS),
∴BF=AE.
点评 此题主要考查了全等三角形的判定与性质以及矩形的性质,得出△BFC≌△EAB是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.将抛物线y=2x2-12x+19绕它的顶点旋转180°后的解析式是( )
| A. | y=-2x2-12x+19 | B. | y=-2x2+12x-19 | C. | y=-2x2+12x-17 | D. | y=-2x2-12x-17 |
15.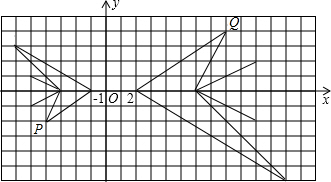 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )| A. | (-2a,-2b) | B. | (-a,-2b) | C. | (-2b,-2a) | D. | (-2a,-b) |
19.已知梯形ABCD中,AD∥BC,则∠A:∠B:∠C:∠D不可能是( )
| A. | 3:7:5:5 | B. | 5:4:5:4 | C. | 4:5:6:3 | D. | 8:1:4:5 |
20.下列各式正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\sqrt{(-7)^{2}}$=7 | C. | $\root{3}{9}$=3 | D. | (-$\sqrt{2}$)2=4 |
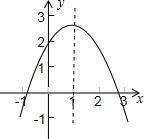 已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( ) 已知:AB∥CD,EF∥CD,且∠ABC=20°,∠CFE=30°,则∠BCF的度数是50°.
已知:AB∥CD,EF∥CD,且∠ABC=20°,∠CFE=30°,则∠BCF的度数是50°. 已知:如图,AB⊥BD,AD⊥AB,∠D=100°,AC平分∠BCD,求∠DAC的度数.
已知:如图,AB⊥BD,AD⊥AB,∠D=100°,AC平分∠BCD,求∠DAC的度数. 如图,∠1+∠2=145度.
如图,∠1+∠2=145度.