题目内容
5.$\frac{{-1+\sqrt{5}}}{2}$的绝对值等于$\frac{-1+\sqrt{5}}{2}$,倒数等于$\frac{\sqrt{5}+1}{2}$.分析 因为$\sqrt{5}$>1,所以$\frac{-1+\sqrt{5}}{5}$为正数,它的绝对值为本身;倒数为$\frac{2}{-1+\sqrt{5}}$,要进行分母有理化.
解答 解:∵$\sqrt{5}$>1,
∴$-1+\sqrt{5}>0$
∴$\frac{-1+\sqrt{5}}{2}$为正数,
∴$\frac{-1+\sqrt{5}}{2}$的绝对值为$\frac{-1+\sqrt{5}}{2}$,
倒数为$\frac{2}{-1+\sqrt{5}}$=$\frac{2(\sqrt{5}+1)}{(-1+\sqrt{5})(\sqrt{5}+1)}=\frac{2(\sqrt{5}+1)}{5-1}=\frac{\sqrt{5}+1}{2}$.
故答案为:$\frac{-1+\sqrt{5}}{2}$;$\frac{\sqrt{5}+1}{2}$.
点评 本题考查了分母有理化,解决本题的关键是运用平方差公式进行分母有理化.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
15.若关于x的不等式(a+1)x>a+1的解集是x<1,则a的取值范围是( )
| A. | a<-1 | B. | a>-1 | C. | a<1 | D. | a<0 |
16.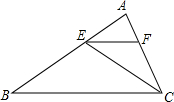 如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
 如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )
如图,CE是△ABC的角平分线,EF∥BC,交AC于点F.已知∠AFE=64°,则∠FEC的度数为( )| A. | 64° | B. | 32° | C. | 36° | D. | 26° |
20.下列方程没有实数根的是( )
| A. | x2+3x+4=0 | B. | (x-2)2=5 | C. | 2x2+7x-1=0 | D. | x2+5x+3=0 |
14.今年3月21日到武汉大学赏樱花的人数约为213000人,数213000用科学记数法表示为( )
| A. | 21.3×104 | B. | 213×103 | C. | 2.13×105 | D. | 2.13×104 |
15.为了解某毕业班学生的睡眠时间情况,小红随机调查了该班15名同学,结果如表,则这15名同学每天睡眠时间的众数是8小时,中位数是8小时.
| 每天睡眠时间(单位:小时) | 7 | 7.5 | 8 | 8.5 | 9 |
| 人 数 | 2 | 4 | 5 | 3 | 1 |
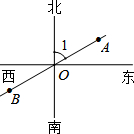 如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.
如图,已知A、B、O三点在同一条直线上,∠1=60°,则射线OA是表示北偏东60°方向的一条射线;射线OB是表示南偏西60°方向的一条射线.