题目内容
10.①已知a+b=5,ab=7,求$\frac{{{a^2}+{b^2}}}{2}$的值;②已知(a+b)2=10,(a-b)2=2,求a2+b2,ab的值.
分析 ①原式分子利用完全平方公式变形,将已知等式代入计算即可求出值;
②已知等式利用完全平方公式展开,相加减即可求出所求式子的值.
解答 解:①∵a+b=5,ab=7,
∴原式=$\frac{(a+b)^{2}-2ab}{2}$=$\frac{25-14}{2}$=$\frac{11}{2}$;
②∵(a+b)2=a2+b2+2ab=10,(a-b)2=a2+b2-2ab=2,
∴两式相加得:a2+b2=6,两式相减得:ab=2.
点评 此题考查了完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
18. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).
一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正方形覆盖部分的面积是( )(用含a,b的代数式表示).| A. | ab | B. | 2ab | C. | a2-ab | D. | b2+ab |
20.相交两圆的圆心距是5,如果其中一个圆的半径是3,那么另外一个圆的半径可以是( )
| A. | 2 | B. | 5 | C. | 8 | D. | 10 |
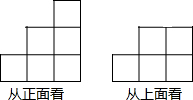 由一些大小相同的小正方体组成的简单几何体从正面和上面看到的形状图象如图所示.
由一些大小相同的小正方体组成的简单几何体从正面和上面看到的形状图象如图所示.