题目内容
9.已知分式$\frac{1-{x}^{2}}{(1+xy)^{2}-(x+y)^{2}}$,判断此分式的值能否为零,说明理由.分析 分式的值为0,则分式的分子为0且分母不为0.
解答 解:令1-x2=0,
解得:x=1或x=-1.
将x=1代入得:$\frac{1-{1}^{2}}{(1+y)^{2}-(1+y)^{2}}$=$\frac{0}{0}$,分式无意义;
将x=-1代入得:$\frac{1-(-1)^{2}}{(1-y)^{2}-(-1+y)^{2}}$=$\frac{0}{0}$,分式无意义.
∴分式的值不能为0.
点评 本题主要考查的是分式值为0的条件,掌握分式值为0的条件是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知A($\sqrt{2}$,1)是正比例函数图象上一点,此函数图形与x轴正半轴夹角α的cosα的值为( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
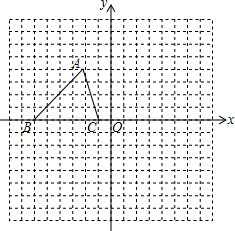 如图,已知的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)
如图,已知的三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0)