题目内容
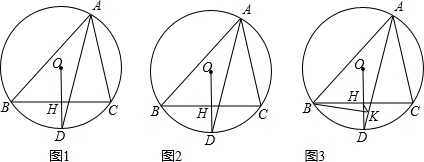
1.已知△ABC中,AC=10,AB=17,BC边上的高线AD=8,求△ABC的面积.分析 分别在两个直角三角形中求得线段BD和线段CD的长,然后求得BC的长,从而求得面积.
解答  解:如图1,在直角三角形ABD中,AB=17,AD=8,
解:如图1,在直角三角形ABD中,AB=17,AD=8,
根据勾股定理,得BD=15;
在直角三角形ACD中,AC=10,AD=8,
根据勾股定理,得CD=6;
∴BC=15+6=21,
∴△ABC的面积为$\frac{1}{2}$×21×8=84;
如图2,在直角三角形ABD中,AB=17,AD=8,
根据勾股定理,得BD=15;
在直角三角形ACD中,AC=10,AD=8,
根据勾股定理,得CD=6;
∴BC=15-6=9,
∴△ABC的面积为$\frac{1}{2}$×9×8=36;
综上所述,△ABC的面积为84或36.
点评 此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度,本题因给出了图形,故只有一种情况.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
18.下列说法正确的是( )
| A. | 两角及一边分别相等的两个三角形全等 | |
| B. | 两边及一角分别相等的两个三角形全等 | |
| C. | 两腰分别相等的两个等腰三角形全等 | |
| D. | 底边及一腰分别相等的两个等腰三角形全等 |

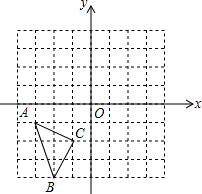 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),