题目内容
13.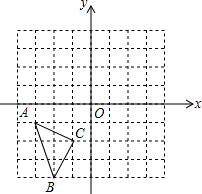 在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),
在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标(-3,-1),(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,并写出B1的坐标;
(2)画出△ABC关于y轴对称的△A2B2C2,并写出C2的坐标;
(3)画出△ABC关于原点对称的△A3B3C3,并写出A3的坐标;
(4)求△ABC的面积.
分析 (1)利用平移的性质,写出点A、B、C的对应点A1、B1、C1的坐标,然后描点即可得到△A1B1C1;
(2)利用关于y轴对称的点的坐标特征,写出点A、B、C的对应点A2、B2、C2的坐标,然后描点即可得到△A2B2C2;
(3)利用平移的性质,写出点A、B、C的对应点A3、B3、C3的坐标,然后描点即可得到△A3B3C3;
(4)利用面积的和差计算△ABC的面积.
解答 解:(1)如图,△A1B1C1为所作,点B1的坐标为((-3,2);
(2)如图,△A2B2C2为所作,点C2的坐标为(1,-2);
(3)如图,△A3B3C3为所作,点A3的坐标为(3,1);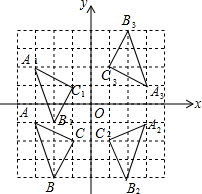
(4)△ABC的面积=2×3-$\frac{1}{2}$×2×-$\frac{1}{2}$×2×1-$\frac{1}{2}$×1×3=$\frac{5}{2}$.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移和轴对称变换.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
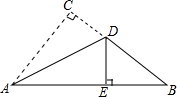 如图,是一张直角三角形的纸片,∠C=90°,AC=6cm,BC=8cm,现将△ABC折叠,使直角顶点C落在斜边AB上,求重叠部分的面积.
如图,是一张直角三角形的纸片,∠C=90°,AC=6cm,BC=8cm,现将△ABC折叠,使直角顶点C落在斜边AB上,求重叠部分的面积. 如图,EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.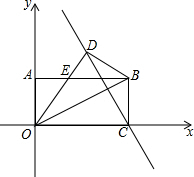 如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.
如图,矩形OABC在平面直角坐标系中,OA=2,∠BOC=30°,把△OBC沿OB对折,点C落在点D处,线段OD与AB交于点E.若点P在直线CD上,并且△OEP为直角三角形,求P点坐标.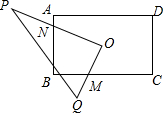 如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.
如图,矩形ABCD中,AB=4,AD=6,O为矩形ABCD的中心,将直角三角形的直角顶点与O重合,一条直角边OP与OA重合,使三角板沿逆时针方向绕点O旋转,两条直角边始终与边BC、AB相交,交点分别为M、N.若BM=x,AN=y,则y与x之间的函数关系式是y=$\frac{3}{2}$x-$\frac{5}{2}$.